CAT 2018 Question Paper | Quants Slot 2

CAT Questions

The topic of Geometry in the Quantitative Aptitude section of the CAT exam is one of the most important topics. The CAT exam is known to test students heavily on Geometry, especially on the triangles section. One cannot simply ignore this topic. A complete understanding and loads of practice can help in gearing of for the CAT exam.Solve CAT Previous Year Paper by visitng 2IIM's CAT Question Bank.

Question 9 :Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,... will be

1. 192√3
2. 164√3
3. 248√3
4. 188√3

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Geometry

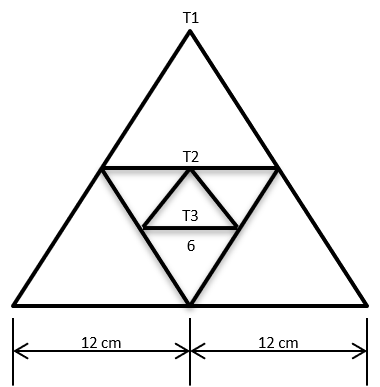
As the triangle progresses infinitely and the side length decreases, it follows an infinite GP series
As the sides decrease by half, their areas decrease by \\frac{1}{4})
We know, Area of an Equilateral Triangle = \\frac{√3}{4}) × a²
Area of T1 = \\frac{√3}{4}) × 24 × 24 = 144 √3 sq cms
Sum of an Infinite GP = \\frac{𝑎}{1−𝑟}) where a = 144 √3 , r = \\frac{1}{4})
Sum of areas ( T1, T2, T3,..) = \\frac{144√3}{1 - \frac{1}{4}}) = \\frac{4 × 144 √3}{3})
Therefore, Sum of areas= 192 √3 sq cms.

The question is " Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, Find the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,.. Then the sum of areas will be equal to 192 √3 sq cms "

Hence, the answer is 192 √3 sq cms.

Choice A is the correct answer.