CAT 2024 Question Paper | Quant Slot 3

CAT Questions

CAT 2024 Quant was dominated by Algebra followed by Arithmetic. In Arithmetic, the questions were dominated by topics like Speed-time-distance, Mixture and Alligations. This year, there was a surprise. The questions from Geometry were relatively on the lower side as compared to the previous years. There were 8 TITA Qs this year. Overall this section was at a medium level of difficulty.

Question 18 The number of distinct real values of \(x\), satisfying the equation \(\max \{x, 2\}-\min \{x, 2\}=|x+2|-|x-2|\), is

---

---

Video Explanation

---

---

Explanatory Answer

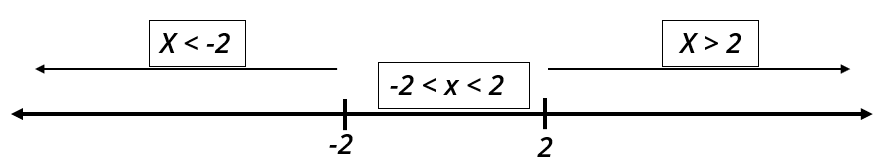
LHS:
\(\max \{x, 2\}-\min \{x, 2\}\) has two segments.
i. \(x>2 \Rightarrow \max \{x, 2\}-\min \{x, 2\}=x-2\)
ii. \(x\) \(<\) \(2\) \(\Rightarrow \max \{x, 2\}-\min \{x, 2\}=2-x\)
RHS:
\(|x+2|-|x-2|\) has three segments.
i. \(\quad x>2\), both \(|x+2| \&|x-2|\) are positive
\[ \Rightarrow|x+2|-|x-2|=(x+2)-(x-2)=4 \] ii. \(x\) \(<\) \(-2\), both \(|x+2| \&|x-2|\) are negative
\[ \Rightarrow|x+2|-|x-2|=-(x+2)-(2-x)=-4 \]
iii. \(-2<\) \(x<\)\(2,|x+2|\) is positive \(\&|x-2|\) is negative \(\Rightarrow|x+2|-|x-2|=(x+2)-(2-x)=2 x\)

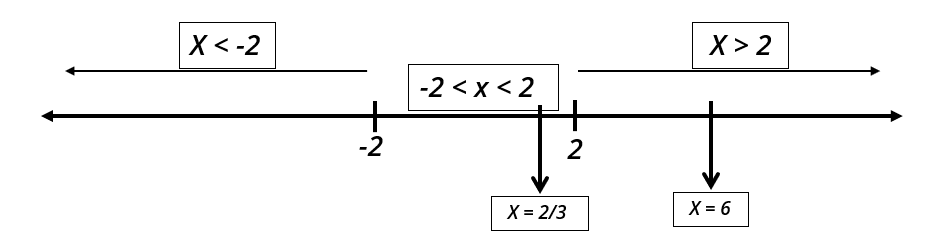
Now comparing both the sides,
When \(x>2\),
\[ x-2=4 \] \(x=6\) [it lies in the range \(x\) \(<\) \(2\) ]
When \(x\) \(<\) \(2\), \[ \begin{array}{l} 2-x=2 x \\ 2=3 x \end{array} \]
\(x=2 / 3\) [it lies in the range \(x\) \(<\) \(2\) ]
Also, when \(x\) \(<\) \(2\), \[ 2-x=-4 \] \(x=6\) [it does not lie in the range \(x\) \(<\) \(2\) ]
So, only 2 distinct real values of \(x\) are possible.

---

The question is "The number of distinct real values of \(x\), satisfying the equation \(\max \{x, 2\}-\min \{x, 2\}=|x+2|-|x-2|\), is "

Hence, the answer is '2'

Verbal Ability for CAT | CAT Reading Comprehension

Verbal Ability for CAT| CAT Para Jumble

Verbal Ability for CAT | CAT Sentence Elimination

Verbal Ability for CAT | CAT Paragraph Completion

Verbal Ability for CAT | CAT Critical Reasoning

Verbal Ability for CAT | CAT Word Usage

Verbal Ability for CAT| CAT Para Summary

Verbal Ability for CAT | CAT Text Completion

Verbal Ability for CAT | CAT Sentence Correction