CAT 2017 Question Paper | CAT LR DI
CAT Question Paper | CAT Previous Year Paper
CAT DI LR section has become increasingly tough beginning from 2015. DILR used to have distinct Data Interpretation sets and Logical reasoning puzzles. It used to be about computation and ability to read charts, graphs and tables for the Data Interpretation and Logical reasoning used to have Family tree, grid puzzles, arrangement, tournaments, cubes as some standard forms of puzzles.Since 2015 this pattern has been broken. With passing years, even the distinction between DI and LR has come down significantly. CAT 2017 Slot 1 had 8 interesting DI and LR puzzle sets. Solving these could be the best way to understand the constitution of the DILR section
CAT DILR : CAT 2017 Question Paper Slot 1
Set 1: Airlines Company
A new airlines company is planning to start operations in a country. The company
has identified ten different cities which they plan to connect through their network to start
with. The flight duration between any pair of cities will be less than one hour. To start
operations, the company has to decide on a daily schedule.
The underlying principle that
they are working on is the following:
Any person staying in any of these 10 cities
should be able to make a trip to any other city in the morning and should be able to return by
the evening of the same day.
-
CAT Previous year paper - CAT Exam DI LR
If the underlying principle is to be satisfied in such a way that the journey between any two cities can be performed using only direct (non-stop) flights, then the minimum number of direct flights to be scheduled is:
-
CAT Previous year paper - CAT Exam DI LR
Suppose three of the ten cities are to be developed as hubs. A hub is a city which is connected with every other city by direct flights each way, both in the morning as well as in the evening. The only direct flights which will be scheduled are originating and/or terminating in one of the hubs. Then the minimum number of direct flights that need to be scheduled so that the underlying principle of the airline to serve all the ten cities is met without visiting more than one hub during one trip is:
![CAT DI LR 2017 Slot 1]()
-
CAT Previous year paper - CAT Exam DI LR
Suppose the 10 cities are divided into 4 distinct groups G1, G2, G3, G4 having 3, 3, 2 and 2 cities respectively and that G1 consists of cities named A, B and C. Further, suppose that direct flights are allowed only between two cities satisfying one of the following:
1. Both cities are in G1
2. Between A and any city in G2
3. Between B and any city in G3
4. Between C and any city in G4
Then the minimum number of direct flights that satisfies the underlying principle of the airline is: (TITA)
-
CAT Previous year paper - CAT Exam DI LR
Suppose the 10 cities are divided into 4 distinct groups G1, G2, G3, G4 having 3, 3, 2 and 2 cities respectively and that G1 consists of cities named A, B and C. Further, suppose that direct flights are allowed only between two cities satisfying one of the following:
1. Both cities are in G1
2. Between A and any city in G2
3. Between B and any city in G3
4. Between C and any city in G4
However, due to operational difficulties at A, it was later decided that the only flights that would operate at A would be those to and from B. Cities in G2 would have to be assigned to G3 or to G4.
What would be the maximum reduction in the number of direct flights as compared to the situation before the operational difficulties arose? (TITA)
Set 2 : Cars Travel Route
Four cars need to travel from Akala (A) to Bakala (B). Two routes are available,
one via Mamur (M) and the other via Nanur (N). The roads from A to M, and from N to B, are both
short and narrow. In each case, one car takes 6 minutes to cover the distance, and each
additional car increases the travel time per car by 3 minutes because of congestion. (For
example, if only two cars drive from A to M, each car takes 9 minutes.) On the road from A to N,
one car takes 20 minutes, and each additional car increases the travel time per car by 1 minute.
On the road from M to B, one car takes 20 minutes, and each additional car increases the travel
time per car by 0.9 minute.
The police department orders each car to take a particular
route in such a manner that it is not possible for any car to reduce its travel time by not
following the order, while the other cars are following the order.
-
CAT Previous year paper - CAT Exam DI LR
How many cars would be asked to take the route A-N-B, that is Akala-Nanur-Bakala route, by the police department? (TITA)
-
CAT Previous year paper - CAT Exam DI LR
If all the cars follow the police order, what is the difference in travel time (in minutes) between a car which takes the route A-N-B and a car that takes the route A-M-B?
-
CAT Previous year paper - CAT Exam DI LR
A new one-way road is built from M to N. Each car now has three possible routes to travel from A to B: A-M-B, A-N-B and A-M-N-B. On the road from M to N, one car takes 7 minutes and each additional car increases the travel time per car by 1 minute. Assume that any car taking the A-M-N-B route travels the A-M portion at the same time as other cars taking the A-M-B route, and the N-B portion at the same time as other cars taking the A-N-B route.
How many cars would the police department order to take the A-M-N-B route so that it is not possible for any car to reduce its travel time by not following the order while the other cars follow the order? (Assume that the police department would never order all the cars to take the same route.) (TITA)
-
CAT Previous year paper - CAT Exam DI LR
A new one-way road is built from M to N. Each car now has three possible routes to travel from A to B: A-M-B, A-N-B and A-M-N-B. On the road from M to N, one car takes 7 minutes and each additional car increases the travel time per car by 1 minute. Assume that any car taking the A-M-N-B route travels the A-M portion at the same time as other cars taking the A-M-B route, and the N-B portion at the same time as other cars taking the A-N-B route.
If all the cars follow the police order, what is the minimum travel time (in minutes) from A to B? (Assume that the police department would never order all the cars to take the same route.)
Set 3 : Common Entrance Test
Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and
Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test
has three sections: Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET,
those at or above the 80th percentile in at least two sections, and at or above the 90th
percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used
by AIE for final selection.
For the 200 candidates who are at or above the 90th
percentile overall based on CET, the following are known about their performance in CET:
1.No one is below the 80th percentile in all 3 sections.
2.150 are at or above the 80th
percentile in exactly two sections.
3.The number of candidates at or above the 80th
percentile only in P is the same as the number of candidates at or above the 80th percentile
only in C. The same is the number of candidates at or above the 80th percentile only in M.
4.Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in
C: Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process
for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score
for final selection provided the candidate is at or above the 80th percentile in P. Any other
candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is
required to appear in a separate test to be conducted by BIE for being considered for final
selection. Altogether, there are 400 candidates this year who are at or above the 80th
percentile in P.
-
CAT Previous year paper - CAT Exam DI LR
What best can be concluded about the number of candidates sitting for the separate test for BIE who were at or above the 90th percentile overall in CET?
-
CAT Previous year paper - CAT Exam DI LR
If the number of candidates who are at or above the 90th percentile overall and also at or above the 80th percentile in all three sections in CET is actually a multiple of 5, what is the number of candidates who are at or above the 90th percentile overall and at or above the 80th percentile in both P and M in CET? (TITA)
-
CAT Previous year paper - CAT Exam DI LR
If the number of candidates who are at or above the 90th percentile overall and also at or above the 80th percentile in all three sections in CET is actually a multiple of 5, then how many candidates were shortlisted for the AET for AIE? (TITA)
-
CAT Previous year paper - CAT Exam DI LR
If the number of candidates who are at or above the 90th percentile overall and also are at or above the 80th percentile in P in CET, is more than 100, how many candidates had to sit for the separate test for BIE?
Set 4 : Fast Food Joint
Healthy Bites is a fast food joint serving three items: burgers, fries and ice
cream. It has two employees Anish and Bani who prepare the items ordered by the clients.
Preparation time is 10 minutes for a burger and 2 minutes for an order of ice cream. An employee
can prepare only one of these items at a time. The fries are prepared in an automatic fryer
which can prepare up to 3 portions of fries at a time, and take 5 minutes irrespective of the
number of portions. The fryer does not need an employee to constantly attend to it, and we can
ignore time taken by an employee to start and stop the fryer; thus, an employee can be engaged
in preparing other items while the frying is on. However, fries cannot be prepared in
anticipation of future orders.
Healthy Bites wishes to serve the orders as early as
possible. The individual items in any orders are served as and when ready; however, the order is
considered to be completely served only when all the items of that order are served.
The table below gives the orders of three clients and the times at which they placed their
orders:

-
CAT Previous year paper - CAT Exam DI LR
Assume that only one client’s order can be processed at any given point of time. So, Anish or Bani cannot start preparing a new order while previous order is being prepared.
At what time is the order placed by client 1 completely served?
-
CAT Previous year paper - CAT Exam DI LR
Assume that only one client’s order can be processed at any given point of time. So, Anish or Bani cannot start preparing a new order while previous order is being prepared.
At what time is the order placed by client 3 completely served?
-
CAT Previous year paper - CAT Exam DI LR
Suppose the employees are allowed to process multiple orders at a time, but the preference would be to finish orders of clients who placed their orders earlier.
At what time is the order placed by client 2 completely served?
-
CAT Previous year paper - CAT Exam DI LR
Suppose the employees are allowed to process multiple orders at a time, but the preference would be to finish orders of clients who placed their orders earlier.
Also assume that the fourth client came in only at 10:35. Between 10:00 and 10:30, for how many minutes is exactly one of the employees idle?
Set 5 : Rural Kids Survey
A study to look at the early learning of rural kids was carried out in a number of
village spanning three states, chosen from the North East (NE), the West (W) and the South (S).
50 four-year old kids each were sampled from each of the 150 villages from NE, 250 villages from
W and 200 villages from S. It was found that of the 30000 surveyed kids 55% studied in primary
schools run by government (G), 37% in private schools (P) while the remaining 8% did not go to
school (O).
The kids surveyed were further divided into two groups based on whether
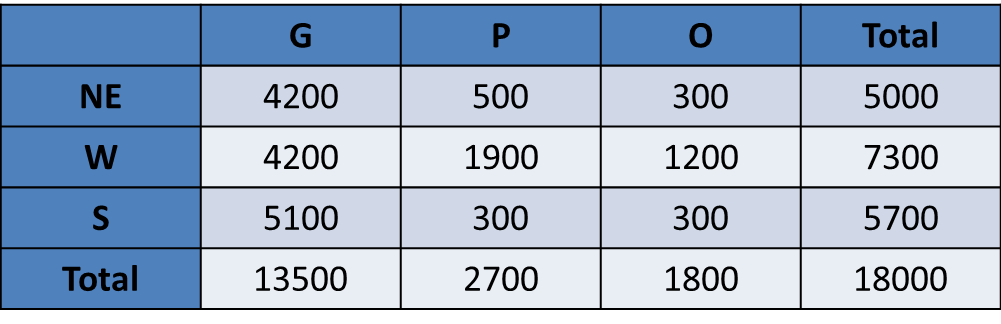
their mothers dropped out of school before completing primary education or not. The table below
gives the number of kids in different type of schools for mothers who dropped out of school
before completing primary education:
It is also known that:
1.In S, 60% of the surveyed kids were in G. Moreover, in S,
all surveyed kids whose mothers had completed primary education were in school.
2.In NE,
among the O kids, 50% had mothers who had dropped out before completing primary education.
3.The number of kids in G in NE was the same as the number of kids in G in W.
-
CAT Previous year paper - CAT Exam DI LR
What percentage of kids from S were studying in P?
-
CAT Previous year paper - CAT Exam DI LR
Among the kids in W whose mothers had completed primary education, how many were not in school?
-
CAT Previous year paper - CAT Exam DI LR
In a follow up survey of the same kids two years later, it was found that all the kids were now in school. Of the kids who were not in school earlier, in one region, 25% were in G now, whereas the rest were enrolled in P; in the second region, all such kids were in G now; while in the third region, 50% of such kids had now joined G while the rest had joined P. As a result, in all three regions put together, 50% of the kids who were earlier out of school had joined G. It was also seen that no surveyed kid had changed schools.
What number of the surveyed kids now were in G in W?
-
CAT Previous year paper - CAT Exam DI LR
In a follow up survey of the same kids two years later, it was found that all the kids were now in school. Of the kids who were not in school earlier, in one region, 25% were in G now, whereas the rest were enrolled in P; in the second region, all such kids were in G now; while in the third region, 50% of such kids had now joined G while the rest had joined P. As a result, in all three regions put together, 50% of the kids who were earlier out of school had joined G. It was also seen that no surveyed kid had changed schools.
What percentage of the surveyed kids in S, whose mothers had dropped out before completing primary education, were in G now?
Set 6 : Simple Happiness Index
Simple Happiness index (SHI) of a country is computed on the basis of three
parameters: social support (S), freedom to life choices (F) and corruption perception (C). Each
of these three parameters is measured on a scale of 0 to 8 (integers only). A country is then
categorized based on the total score obtained by summing the scores of ail the three parameters,
as shown in the following table:

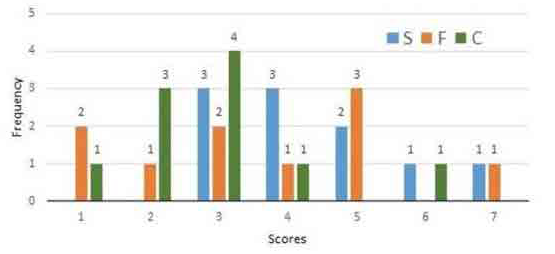
Following diagram depicts the frequency distribution of the scores in S, F
and C of 10 countries - Amda, Benga, Calla, Delma, Eppa, Varsa, Wanna, Xanda, Yanga and Zooma:
Further, the following are
known:
1.Amda and Calla jointly have the lowest total score, 7, with identical scores in all
the three parameters.
2.Zooma has a total score of 17.
3.All the 3 countries, which
categorised as happy, have the highest score in exactly one parameter.
-
CAT Previous year paper - CAT Exam DI LR
What is Amda's score in F? (TITA)
-
CAT Previous year paper - CAT Exam DI LR
What is Zooma's score in S? (TITA)
-
CAT Previous year paper - CAT Exam DI LR
Benga and Delma, two countries categorized as happy, are tied with the same total score. What is the maximum score they can have?
-
CAT Previous year paper - CAT Exam DI LR
If Benga scores 16 and Delma scores 15, then what is the maximum number of countries with a score of 13?
Set 7 : Square Layout
In a square layout of size 5m × 5m, 25 equal sized square platforms of different
heights are built. The heights (in metres) of individual platforms are as shown below:
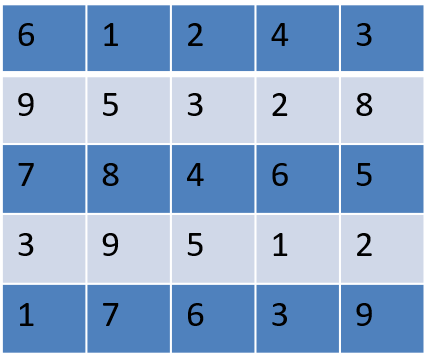
Individuals (all of same
height) are seated on these platforms. We say an individual A can reach an individual B if all
the three following conditions are met:
i.) A and B are In the same row or column
ii.) A is at a lower height than B
iii.) If there is/are any individual(s) between A and B,
such individual(s) must be at a height lower than that of A.
Thus in the table given
above, consider the Individual seated at height 8 on 3rd row and 2nd column. He can be reached
by four individuals. He can be reached by the individual on his left at height 7, by the two
individuals on his right at heights of 4 and 6 and by the individual above at height 5. Rows in
the layout are numbered from top to bottom and columns are numbered from left to right.
-
CAT Previous year paper - CAT Exam DI LR
How many individuals in this layout can be reached by just one individual?
-
CAT Previous year paper - CAT Exam DI LR
Which of the following is true for any individual at a platform of height 1m in this layout?
- They can be reached by all the individuals in their own row and column.
- They can be reached by at least 4 individuals.
- They can be reached by at least one individual.
- They cannot be reached by anyone.
-
CAT Previous year paper - CAT Exam DI LR
We can find two individuals who cannot be reached by anyone in
-
CAT Previous year paper - CAT Exam DI LR
Which of the following statements is true about this layout?
- Each row has an individual who can be reached by 5 or more individuals
- Each row has an individual who cannot be reached by anyone
- Each row has at least two individuals who can be reached by an equal number of individuals
- All individuals at the height of 9 m can be reached by at least 5 individuals
Set 8 : Team Project
There are 21 employees working in a division, out of whom 10 are special-skilled
employees (SE) and the remaining are regular skilled employees (RE). During the next five
months, the division has to complete five projects every month. Out of the 25 projects, 5
projects are "challenging", while the remaining ones are "standard". Each of the challenging
projects has to be completed in different months. Every month, five teams - T1, T2, T3, T4 and
T5, work on one project each. T1, T2, T3, T4 and T5 are allotted the challenging project in the
first, second, third, fourth and fifth month, respectively. The team assigned the challenging
project has one more employee than the rest.
In the first month, T1 has one more SE than
T2, T2 has one more SE than T3, T3 has one more SE than T4, and T4 has one more SE than T5.
Between two successive months, the composition of the teams changes as follows:
a. The
team allotted the challenging project, gets two SE from the team which was allotted the
challenging project in the previous month. In exchange, one RE is shifted from the former team
to the latter team.
b. After the above exchange, if T1 has any SE and T5 has any RE,
then one SE is shifted from T1 to T5, and one RE is shifted from T 5 to T1. Also, if T2 has any
SE and T4 has any RE, then one SE is shifted from T2 to T4, and one RE is shifted from T4 to
T2.
Each standard project has a total of 100 credit points, while each challenging
project has 200 credit points. The credit points are equally shared between the employees
included in that team.
-
CAT Previous year paper - CAT Exam DI LR
The number of times in which the composition of team T2 and the number of times in which composition of team T4 remained unchanged in two successive months are:
-
CAT Previous year paper - CAT Exam DI LR
The number of SE in T1 and T5 for the projects in the third month are, respectively:
-
CAT Previous year paper - CAT Exam DI LR
Which of the following CANNOT be the total credit points earned by any employee from the projects?
-
CAT Previous year paper - CAT Exam DI LR
One of the employees named Aneek scored 185 points. Which of the following CANNOT be true?
- Aneek worked only in teams T1, T2, T3, and T4
- Aneek worked only in teams T1, T2, T4, and T5
- Aneek worked only in teams T2, T3, T4, and T5
- Aneek worked only in teams T1, T3, T4, and T5