CAT 2018 Question Paper | CAT LR DI

CAT Questions

The questions that ask you to find the incorrect statement among the choices are generally time-consuming because you need to test the validity of each statement individually and then come to a final conclusion. This is one such question from the Product and Companies puzzle set that appeared in the CAT 2018 question paper. The difficulty of this question is medium to hard owing to the arduous demands of the puzzle. Check out this wonderful question from CAT previous year paper and hone your DILR skills.

CAT DILR : CAT 2018 Question Paper Slot 2

Set 3 : Fun Sports Club

Fun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:
1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.
2. There are a total of 17 students enrolled in G.
3. The number of students enrolled only in G is one less than the number of students enrolled only in L.
4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.
5. The maximum student enrollment is in L.
6. Ten students enrolled in G are also enrolled in at least one more sport.

Question 3 : Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and K? [TITA]

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question on CAT DILR

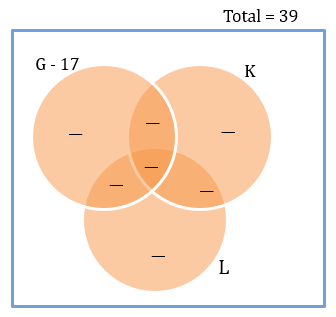
From condition 3, we get the above diagram.

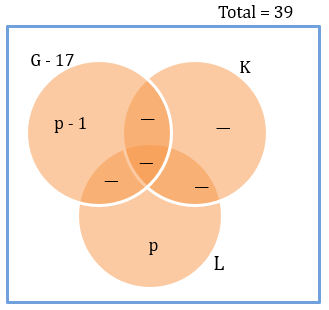
Condition 6 tells us p – 1 = 7. G-total = 17. G and something else = 10. G-only should be 7.

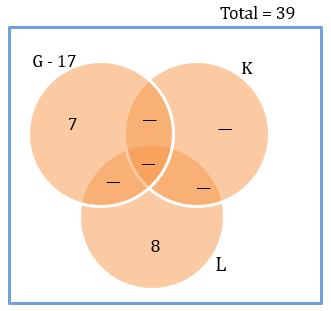
From condition 1, we get the above diagram.

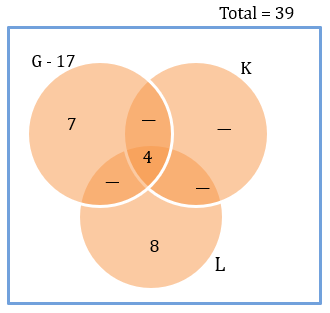
From condition 6, we can get the diagram.

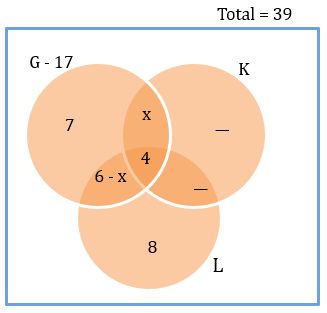
From condition 4, we get the above diagram.

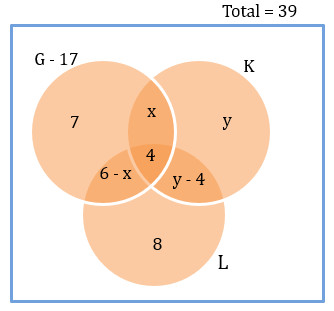
Now we know that the total = 39.

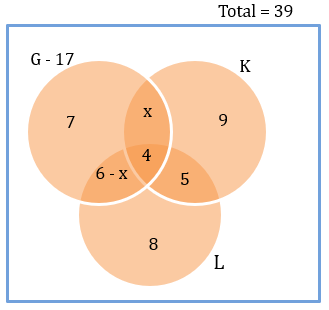
From condition 5,
Number of students in L = 4 + 5 + 8 + 6 – x = 23- x.
Number of students in K = 4 + 5 + 9 + x = 18 + x.
We know that 23 – x > 18 + x.
5 > 2x. x < \\frac{5}{2}).
x could be 0, 1 or 2.


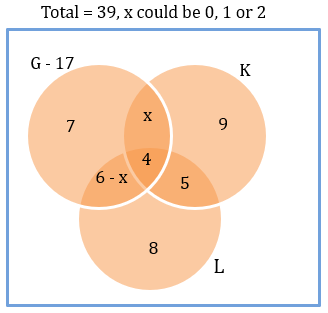
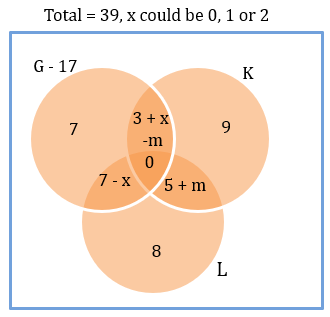
We know that G ∩ K ∩ L = 0. We know that the 4 that were originally here are distributed among the three regions currently having x, 6 – x and 5.
We know that one student leaves K. So, this student should have gone to the region (G and L but not K).
Or, (G and L but not K) will now read 7 – x.
The other three should have opted out of one or the other of G and L. Let us assume m students left G, 3 – m should have left L.
Let us rejig the diagram.
Total number of students in G = 17 – m.
Total number of students in L = 20 + m – x.
20 + m – x – (17 – m) = 3 + 2m – x = 6.
2m – x = 3. x can only take values 0, 1 and 2. 2m = 3 + x.
Or, x has to be 1. m has to be 2.
Both G and K = 3 + x – m. 3 + 1 -2 = 2.

The question is "Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and K? [TITA]"

Hence, the answer is 2