CAT 2023 Question Paper | Quant Slot 1

CAT Questions

CAT 2023 Quant was dominated by Algebra followed by Arithmetic. In Arithmetic, the questions were dominated by topics like Speed-time-distance, Mixture and Alligations. This year, there was a surprise. The questions from Geometry were relatively on the lower side as compared to the previous years. There were 8 TITA Qs this year. Overall this section was at a medium level of difficulty.

Question 17 : Let \(\mathrm{C}\) be the circle \(x^2+y^2+4 x-6 y-3=0\) and \(\mathrm{L}\) be the locus of the point of intersection of a pair of tangents to \(\mathrm{C}\) with the angle between the two tangents equal to \(60^{\circ}\). Then, the point at which \(L\) touches the line \(x=6\) is

---

---

Video Explanation

---

---

Explanatory Answer

\( x ^ { 2 } + y ^ { 2 } + 4 x - 6 y - 3 = 0 \)
\( x ^ { 2 } + 2 \cdot 2 \cdot x + 2 ^ { 2 } - 2 ^ { 2 } + y ^ { 2 } - 2 \cdot 3 \cdot y + 3 ^ { 2 } - 3 ^ { 2 } - 3 = 0 \)
\( ( x + 2 ) ^ { 2 } + ( y - 3 ) ^ { 2 } - \left( 2 ^ { 2 } + 3 ^ { 2 } + 3 \right) = 0 \)
\( ( x + 2 ) ^ { 2 } + ( y - 3 ) ^ { 2 } = 4 ^ { 2 } \)
This is the equation of a circle with radius 4 units and centered at (-2, 3)
From a point L we drop two tangents on the circle such that the angle between the tangents is 60^o.

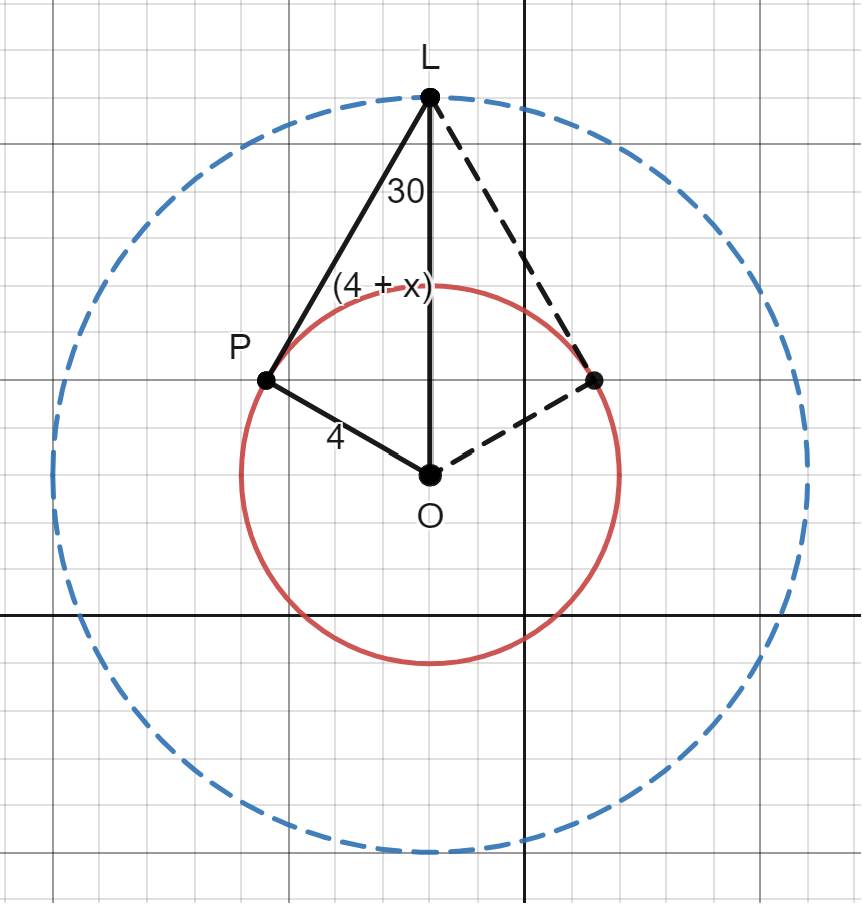
\( \angle L P O = 90 ^ { \circ } \)
\( \angle P L O = 30 ^ { \circ } \)
\( \sin \left( 30 ^ { \circ } \right) = \frac { 1 } { 2 } = \frac { P O } { O L } = \frac { 4 } { 4 + x } \)
\( 4 + x = 2 ( 4 ) \)
\( x = 4 \)
Therefore the locus of the point L, is a circle centered at (-2, 3) and has a radius of (4 + x = 8) units.
The equation of this locus is thus, \( ( x + 2 ) ^ { 2 } + ( y - 3 ) ^ { 2 } = 8 ^ { 2 } \)
When x = 6, we have, \( ( 8 ) ^ { 2 } + ( y - 3 ) ^ { 2 } = 8 ^ { 2 } \), that is y = 3
The circle , \( ( x + 2 ) ^ { 2 } + ( y - 3 ) ^ { 2 } = 8 ^ { 2 } \), touches the line \( x = 6 \) at (6, 3).

---

The answer is '(6,3)'

Choice C is the correct answer.