CAT 2023 Question Paper | Quant Slot 1

CAT Questions

CAT 2023 Quant was dominated by Algebra followed by Arithmetic. In Arithmetic, the questions were dominated by topics like Speed-time-distance, Mixture and Alligations. This year, there was a surprise. The questions from Geometry were relatively on the lower side as compared to the previous years. There were 8 TITA Qs this year. Overall this section was at a medium level of difficulty.

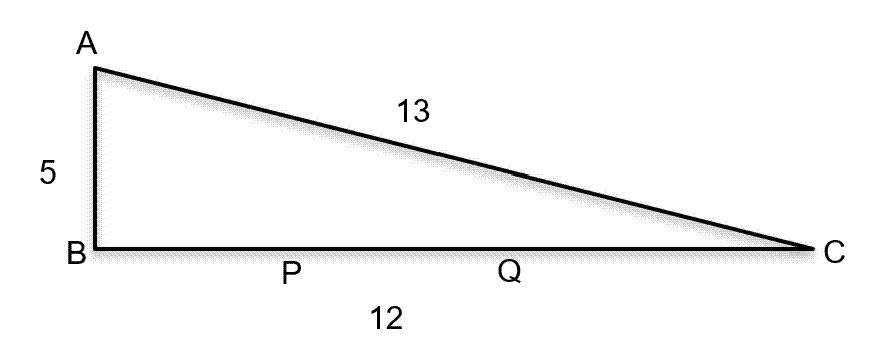
Question 19 : In a right-angled triangle ABC, the altitude AB is 5 cm, and the base BC is 12 cm. P and Q are two points on BC such that the areas of ΔABP, ΔABQ and ΔABC are in arithmetic progression. If the area of ΔABC is 1.5 times the area of ΔABP, the length of PQ, in cm, is

---

---

Video Explanation

---

---

Explanatory Answer

The construction of the triangle according to the question is as follows:

\( A r ( \triangle A B C ) = \frac { 1 } { 2 } 5 \times 12 = 30 \mathrm {~cm} ^ { 2 } \)
\( \operatorname { Ar } ( \triangle A B C ) = 1.5 \times \operatorname { Ar } ( \triangle A B P ) \)
\( \frac { 30 } { 1.5 } = \operatorname { Ar } ( \triangle A B P ) \)
\( \operatorname { Ar } ( \triangle A B P ) = 20 \)
\( \frac { 1 } { 2 } \times A B \times B P = 20 \)
\( B P = \frac { 20 \times 2 } { 5 } = 8 \)
\( \operatorname { Ar } ( \triangle A B P ) , \operatorname { Ar } ( \triangle A B Q ) , \operatorname { Ar } ( \triangle A B C ) \) are in \( A . P \)
\( \operatorname { Ar } ( \triangle A B Q ) = \frac { \operatorname { Ar } ( \triangle A B P ) + \operatorname { Ar } ( \triangle A B C ) } { 2 } = \frac { 20 + 30 } { 2 } = 25 \)
\( \frac { 1 } { 2 } \times 5 \times B Q = 25 \)
\( B Q = \frac { 50 } { 5 } = 10 \)
\( P Q = B Q - B P \)
\( P Q = 10 - 8 = 2 \mathrm {~cm} \)

---

The answer is '2'