IIFT 2022 Question Paper | IIFT Quants

IIFT Quantitative Aptitude | IIFT 2022 Question Paper

The best way to boost your IIFT prep is to practice the actual IIFT Question Papers. 2IIM offers you exactly that, in a student friendly format to take value from this. In the 2022 IIFT, quants were a mixed bag of questions of varying difficulty, with some routine questions and the others were very demanding. Some beautiful questions that laid emphasis on Learning ideas from basics and being able to comprehend more than remembering gazillion formulae and shortcuts.

IIFT 2022 Question Paper QA

Determine what day of the week was on 6th July, 2003 if 10 th July, 2010 was a Thursday?
1. Monday
2. Wednesday
3. Friday
4. Sunday
IIFT 2022 Question Paper QA

A man invests a certain principal amount of money at \( 6.5 \% \) per annum simple interest and another principal amount of money at \( 7.5 \% \) per annum simple interest. Without reinvestment, his income from interest after 3 years is Rs. 400 . One fourth of first principal amount is equal to one fifth of the second principal amount. Find the approximate total sum that was invested.
1. 1890
2. 1050
3. 1140
4. 1560
IIFT 2022 Question Paper QA

A clock is set right at \( 7 \mathrm { AM } \) on 12 th January, 2022 . The clock loses 18 minutes in every 24 hours. What will be the approximate true time when clock indicates 7 PM on 17 th January, 2022?
1. \( 05 : 40 : 15 \) PM
2. \( 05 : 20 : 45 \) PM
3. \( 08 : 20 : 45 \) PM
4. \( 08 : 40 : 15 \) PM
IIFT 2022 Question Paper QA

Two pipes can fill a tank in 12 hours and 18 hours respectively. The pipes are opened simultaneously and it is found that due to leakage at the bottom of the tank, it took 36 minutes more to fill the tank. When the tank is full, in what time the leak will empty it?
1. \( 93.6 \) hours
2. \( 85.4 \) hours
3. \( 104.3 \) hours
4. \( 112.1 \) hours
IIFT 2022 Question Paper QA

A potential recruit gets a total of \( 55 \% \) marks. There are 6 performance parameters with maximum marks of 100 in each parameter. The recruit gets marks in the ratio of 10:9:8:7:6:5 respectively in different parameters. In the first 3 parameters, the criteria for clearing performance score is \( 55 \% \) of the maximum marks and for next 3 parameters is \( 50 \% \) of the maximum marks. How many parameters has the recruit cleared?
1. 5
2. 3
3. 4
4. 6
IIFT 2022 Question Paper QA

The sides of a triangle are 21,20 and \( 13 \mathrm {~cm} \). The given triangle is divided into two triangles by the perpendicular on the longest side from the opposite vertex. What is value of \( 30 \% \) area of the smaller triangle formed?
1. \( 96 \mathrm {~cm} ^ { 2 } \)
2. \( 30 \mathrm {~cm} ^ { 2 } \)
3. \( 9 \mathrm {~cm} ^ { 2 } \)
4. \( 3 \mathrm {~cm} ^ { 2 } \)
IIFT 2022 Question Paper QA

The cost of setting up a utility bag factory is Rs. 1200 . The cost of running the factory is Rs. 125 per 105 bags. The cost of raw material is 80 paise /per bag. The bags are sold at Rs. \( 3.25 \) each. 900 bags were made, but only 785 bags were sold. Other companies can advertise on both sides of the bag. What is the approximate sum to be obtained from the advertisements being printed on the bags, to give a profit of \( 12 \% \) ?
1. Rs. 700
2. Rs. 785
3. Rs. 799
4. Rs. 840
IIFT 2022 Question Paper QA

An investor lent-out a certain sum on simple interest and the same sum on compound interest at the same rate of interest per annum. He noticed that the ratio of the difference of the compound interest and the simple interest for 4 years to the difference of the compound interest and the simple interest for 3 years is \( 20 : 8 \). The approximate rate of interest per annum is given by,
1. \( 69 \% \)
2. \( 54 \% \)
3. \( 77 \% \)
4. \( 41 \% \)
IIFT 2022 Question Paper QA

Find the largest 5 digit number which when divided by 4,9 , and 11 leaves the same but largest remainder for all the three numbers?
1. 99785
2. 99945
3. 99965
4. 99795
IIFT 2022 Question Paper QA

Four sprinters start running from 4 points which are 4 corners of an imaginary rectangle along straight lines and meet at a point ' \( O \) ' which falls inside the rectangle as shown in the figure, after the first three sprinters run \( 55 \mathrm {~m} , 65 \mathrm {~m} \) and \( 75 \mathrm {~m} \) respectively. What is the approximate distance that the fourth sprinter will run to meet the other three sprinters at point \( O \) ?
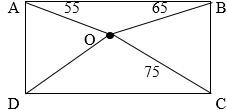
1. \( 66.5 \mathrm {~m} \)
2. \( 50.5 \mathrm {~m} \)
3. \( 48.5 \mathrm {~m} \)
4. \( 68.5 \mathrm {~m} \)
IIFT 2022 Question Paper QA

Let integer \( \alpha \) be one of the roots of \( a x ^ { 2 } + 2 x + 3 = 0 \) and integer \( \beta \) be one of the roots of \( 5 x ^ { 2 } + b x + 8 = 0 \). It is also given that \( \alpha = \beta ^ { 2 } \). Which of the following statement is true if \( b = - 14 \) ?
1. \( 32 b + 8 a ^ { 2 } b - 64 a b = - 175 \)
2. \( 32 a + 16 a b ^ { 2 } + 16 a b = 275 \)
3. \( 64 b + 8 a b ^ { 2 } - 8 a b = 175 \)
4. \( 64 a + 4 a b ^ { 2 } + 32 a b = - 275 \)
IIFT 2022 Question Paper QA

Find the value of \( x \) such that \( ( 1 - x ) ^ { \frac { 3 } { 2 } } + ( 1 + x ) ^ { \frac { 3 } { 2 } } + 2 \sqrt { 1 - x ^ { 2 } } = \left( 2 + 2 \sqrt { 1 - x ^ { 2 } } \right) ^ { \frac { 3 } { 2 } } \)
1. \( \frac { 5 } { 11 } \sqrt { 7 } \)
2. \( \frac { 1 } { 5 } \sqrt { 3 } \)
3. \( \frac { 3 } { 7 } \sqrt { 5 } \)
4. \( \frac { 4 } { 9 } \sqrt { 2 } \)
IIFT 2022 Question Paper QA

An integer is called a perfect square if it is square of another integer. The number of perfect square points (i.e. both coordinates are perfect squares) that lie exactly within the circle \( ( x - 12 ) ^ { 2 } + ( y - 10 ) ^ { 2 } = 64 \) is
1. 8
2. 4
3. 6
4. 1
IIFT 2022 Question Paper QA

An \( n \)-digit number is a positive number with exactly \( n \) digits. Nine hundred distinct \( n \)-digit numbers are to be formed using digits \( 2,3,4,5,7 \) such that each \( n \)-digit number has the

(i) first and last digits are same
(ii) first and third are prime numbers
(iii) second should be greater than or equal to 4 .

What should be the minimum value of \( n \) such that the above is possible?
1. 5
2. 6
3. 7
4. 8
IIFT 2022 Question Paper QA

Pot "A" contains 5 blue and 10 green balls and another pot "B" contains 7 blue and 2 green balls. A biased dice with six sides numbered 1 to 6 is rolled. The probability of each odd outcome is same and the probability of each even outcome is same. But the probability of an odd outcome is twice than the probability of an even outcome. If the face 1 or 2 or 3 comes up, a ball is taken from the pot "A" else a ball is taken from the pot "B". Find the probability of drawing a green ball.
1. \( 38 / 81 \)
2. \( 33 / 81 \)
3. \( 28 / 81 \)
4. \( 25 / 81 \)
IIFT 2022 Question Paper QA

In 1920 , the "Sahitya Shakti" society was established by 500 members who read Premchand. In 1921 , due to internal conflict, it removed all 200 members who also read Shakespeare. In 1922 , further the members who also read Tolstoy numbering 100 left the society. In 1923 , the society added only those ex-members who read both Shakespeare and Premchand but not Tolstoy after which the Sahitya Shakti society consisted of 350 members. Which of the following is true?
1. 200 original members read both Premchand and Tolstoy
2. 50 original members read together Premchand and Shakespeare and Tolstoy
3. 300 original members read both Premchand and Shakespeare but not Tolstoy
4. 150 original members read both Shakespeare and Tolstoy
IIFT 2022 Question Paper QA

It is given that \( P ( A \cup B ) < 3 / 4 , \mathrm { P } ( A )> 1 / 8 , P ( A / B ) < 1 / 2 \). Which of the following is true?
1. \( P ( A \cap B ) + P ( A ) > 7 / 8 \)
2. \( P ( A \cap B ) + P ( A ) > 3 / 4 \)
3. \( P ( A \cap B ) < 5 / 8 \)
4. \( P ( A \cap B ) > 7 / 8 \)
IIFT 2022 Question Paper QA

Find \( \tan ^ { 4 } \alpha + \tan ^ { 4 } \gamma \) using the information given below:
\( \tan ( \theta - \gamma ) = \frac { 1 } { \sqrt { 2 } } , \quad \tan \theta \tan \gamma = \tan ^ { 2 } \alpha \)
1. \( \frac { \tan ^ { 2 } \gamma } { 2 } \left[ \left( \tan ^ { 2 } \alpha + 3 \right) ^ { 2 } - 8 \right] \)
2. \( \frac { \tan ^ { 2 } \gamma } { 2 } \left[ \left( \tan ^ { 2 } \alpha - 3 \right) ^ { 2 } + 8 \right] \)
3. \( \frac { \tan ^ { 2 } \gamma } { 4 } \left[ \left( 3 \tan ^ { 2 } \alpha + 1 \right) ^ { 2 } - 4 \right] \)
4. \( \frac { \tan ^ { 2 } \gamma } { 4 } \left[ \left( 3 \tan ^ { 2 } \alpha - 3 \right) ^ { 2 } + 4 \right] \)
IIFT 2022 Question Paper QA

A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60 degrees. When he retires ' \( y \) ' metre from the bank perpendicular to the tree, he finds the angle to be 45 degrees. When he further retires \( 15 - 5 \sqrt { 3 } \) metre perpendicular to the tree, he finds the angle to be 30 degrees. Find the height of the tree in metres?
1. \( 10 \sqrt { 3 } \)
2. \( 15 + \sqrt { 3 } \)
3. \( 5 \sqrt { 3 } \)
4. \( 15 - \sqrt { 3 } \)
IIFT 2022 Question Paper QA

Let \( a - d , a , a + d , a + 2 d \) be four terms of an arithmetic progression with integer entries and \( a , a + d , a + 2 d , a + 3 d \) be another four terms of the same arithmetic progression. Let \( x = a ( a - d ) ( a + d ) ( a + 2 d ) + d ^ { 4 } \) and \( y = a ( a + d ) ( a + 2 d ) ( a + 3 d ) + d ^ { 4 } \). Then \( x + y \) is equal to ?
1. \( \left( a ^ { 2 } - d ^ { 2 } + 5 a d \right) ^ { 2 } + \left( 2 a ^ { 2 } - 3 a d \right) ^ { 2 } \)
2. \( \left( a ^ { 2 } - 2 d ^ { 2 } + 2 a d \right) ^ { 2 } + \left( 2 a ^ { 2 } - \mathrm { d } ^ { 2 } - a d \right) ^ { 2 } \)
3. \( \left( a ^ { 2 } + 3 d ^ { 2 } - a d \right) ^ { 2 } + \left( a ^ { 2 } + d ^ { 2 } \right) ^ { 2 } \)
4. \( \left( a ^ { 2 } + d ^ { 2 } + 3 a d \right) ^ { 2 } + \left( a ^ { 2 } - d ^ { 2 } + a d \right) ^ { 2 } \)
IIFT 2022 Question Paper QA

A green liquid is mixed with a blue liquid in the proportion \( 4 : 5 \) and the mixture is sold at Rs. 20 per litre at a \( 20 \% \) profit. If the green liquid costs Rs. 4 more per litre than the blue liquid, what does the green liquid cost per litre approximately?
1. Rs. \( 16.33 \)
2. Rs. \( 18.88 \)
3. Rs. \( 17.66 \)
4. Rs. \( 19.22 \)
IIFT 2022 Question Paper QA

Two trains of equal length are running on parallel lines in the same direction at \( 54 \mathrm {~km} / \) hour and \( 40 \mathrm {~km} / \) hour. The slower train started first and then the faster train started after some time. The faster train passes the length of the slower train in 36 seconds completely. The length of each train is?
1. \( 50 \mathrm {~m} \)
2. \( 70 \mathrm {~m} \)
3. \( 80 \mathrm {~m} \)
4. \( 90 \mathrm {~m} \)
IIFT 2022 Question Paper QA

\( \mathrm { AB } \) and \( \mathrm { CD } \) are two chords intersecting at point \( \mathrm { E } \). Ram started from point A with a speed of \( 2 \mathrm {~km} / \mathrm { hr } \). After reaching point \( \mathrm { E } \), Ram moved to point \( \mathrm { D } \) with same speed and covered ED in one-fifth of the time taken for AE. Similarly, Shyam moved from point \( \mathrm { C } \) to point \( \mathrm { B } \) through point \( \mathrm { E } \). If Shyam takes in total 18 hours to cover the whole distance from \( \mathrm { C } \) to \( \mathrm { B } \) through point \( \mathrm { E } \) with same speed, what is the time Shyam took to cover BE?
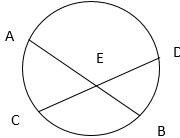
1. \( 1.5 \) hours
2. 2 hours
3. 3 hours
4. \( 4.5 \) hours
IIFT 2022 Question Paper QA

Find the area of the shaded region. Given that \( \mathrm { ABCD } \) is a square with side length ' \( b \) ' units and \( \mathrm { E } \) is the midpoint of \( \mathrm { AB } \).
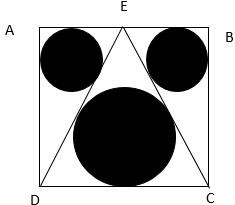
1. \( \frac { \pi b ^ { 2 } } { 4 ^ { 2 } } [ 36 - 16 \sqrt { 3 } ] \)
2. \( \frac { \pi b ^ { 2 } } { 4 ^ { 2 } } [ 34 + 14 \sqrt { 5 } ] \)
3. \( \frac { \pi b ^ { 2 } } { 4 ^ { 2 } } [ 34 - 14 \sqrt { 5 } ] \)
4. \( \frac { \pi b ^ { 2 } } { 4 ^ { 2 } } [ 36 + 16 \sqrt { 3 } ] \)
IIFT 2022 Question Paper QA

A large solid iron sphere of diameter \( 10 \mathrm {~m} \) is melted and \( 2 / 5 \) of the melted amount is recast into several small spheres of diameter \( 2 \mathrm {~m} \). What is the ratio of the total surface area of the smaller spheres and the surface area of the large sphere?
1. \( 1 : 1 \)
2. \( 2 : 1 \)
3. \( 3 : 1 \)
4. \( 4 : 1 \)