XAT 2020 Question Paper | Quantitative Aptitude and Data Interpretation

CAT Questions

The best questions to practice for XAT Exam are the actual XAT Question Papers. 2IIM offers you exactly that, in a student friendly format to take value from this. In XAT 2020 we saw some beautiful questions that laid emphasis on Learning ideas from basics and being able to comprehend more than remembering gazillion formulae and shortcuts. Original XAT Question paper is the best place to start off your XAT prep practice. This page provides exactly that. To check out about 1000 CAT Level questions with detailed video solutions for free, go here: CAT Question Bank

Question 18 : A hare and a tortoise run between points O and P located exactly 6 km from each other on a straight line. They start together at O, go straight to P and then return to O along the same line. They run at constant speeds of 12 km/hr and 1 km/hr respectively. Since the tortoise is slower than the hare, the hare shuttles between O and P until the tortoise goes once to P and returns to O. During the run, how many times are the hare and the tortoise separated by an exact distance of 1 km from each other?

1. 40
2. 24
3. 48
4. 42
5. 22

---

---

---

Explanatory Answer

We are told that the speed of the Tortoise is 1kmph and the speed of the Hare is 12kmph. The distance between O and P is 6 km.

Therefore, for every 1km the Tortoise covers, between O and P, the Hare covers 12 km which is the same distance as a to and fro lap between O and P. This implies that the Hare meets the Tortoise exactly twice every hour, in other words it can also be understood as, for every 1km that the Tortoise covers, the Hare and the Tortoise meet twice.

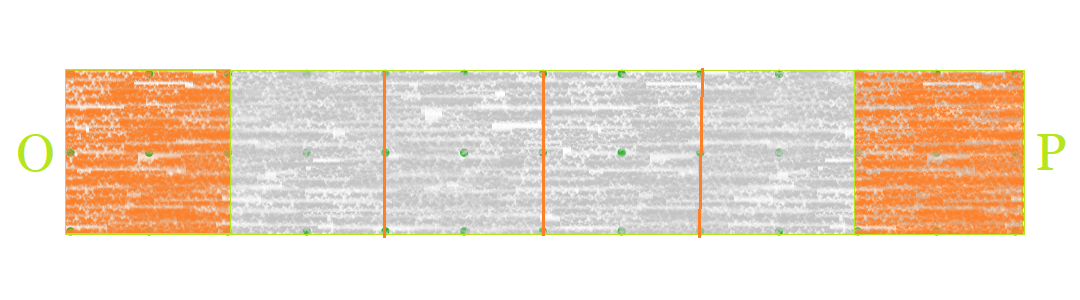
Further, since the meets happen reguraly - every kilometer that the Tortoise covers - ,if we divide the stretch of the distance between O and P into blocks of 1 km each, by the time the Tortoise reaches back to O, there would have been 4 meets in each block except the first block.

Think about the first block, when the Tortoise starts from O to P, the Hare starts simultaeously with it. So, by the time the Tortoise reaches the end of the first block, the Hare would have returned back to O exactly once, and they would have met only once. The same happens in the return journey, when the Tortoise would have been just ready to enter the first block, the Hare would be leaving for a final trip to P. they'd finish on the same point. Altogether there would be exactly 2 meets happening in the first block.
Pictorical representation of the number of meets in each block would be...
But why are we worrying about the meeting points in the first place while the Question is something else???

If the Hare is to the left of the Tortoise before the meet, it will be to the right after the meet(and vice-versa). So for every meet exactly at 2 instances(once on the right and once on the left) the Hare will be 1km away from the Tortoise.

But is it always true??

Not in the first block and the last block. Why? Being in the first block, the Hare can't maintain a distance of 1km from the Tortoise when it is on the left of the Tortoise, similarly it can't maintain a distance of 1km from the Tortoise in the 6th block by being to the right of the Tortoise.

So, the total number of instances where the distance between the Tortoise and the Hare is exactly 1km is 1(2) + 2(4) + 2(4) + 2(4) + 2(4) + 1(4) = 4(0.5 + 2 + 2 + 2 + 2 + 1) = 38.

All this to realize that 38 is not one of the options at all... Good for us.
We didn't take into account 2 instances

1. When the the Hare and the Tortoise start from the same point and as the Hare races away towards P, at some point the distance between them would be 1km
2. Just before the Hare and the Tortoise finish the race, as the they both head towards the finish line at O, there would be an instance, where the distance between them is 1km.

(If this still interests you, since their speeds are in the ratio 1:12, the first case and the second happen when the Hare is at a distance of 12/11 km from O, and the Tortoise 1/11 km from O, both heading towards P in the first case and towards O in the second case.)

Total number of instances = 38 + 2 = 40
Therefore, during the run, the Hare and the Tortoise are separated by an exact distance of 1 km from each other 40 times.

---

Choice A is the correct answer.