XAT 2023 Question Paper | XAT QADI
XAT Quantitative Aptitude & Data Interpretation| XAT 2023 Question Paper
The best questions to practice for XAT Exam are the actual XAT Question Papers. 2IIM offers you exactly that, in a student friendly format to take value from this. If you would like to take the actual CAT papers inside a testing engine (for Free) head out here: CAT Official Question Mocks. In XAT 2023 we saw some beautiful questions that laid emphasis on Learning ideas from basics and being able to comprehend more than remembering gazillion formulae and shortcuts. Original XAT Question paper is the best place to start off your XAT prep practice. This page provides exactly that. To check out about 1000 CAT Level questions with detailed video solutions for free, go here: CAT Question Bank
-
XAT 2023 Question Paper QA DI
Amit has forgotten his 4-digit locker key. He remembers that all the digits are positive integers and are different from each other. Moreover, the fourth digit is the smallest and the maximum value of the first digit is 3. Also, he recalls that if he divides the second digit by the third digit, he gets the first digit. How many different combinations does Amit have to try for unlocking the locker?
-
XAT 2023 Question Paper QA DI
The problem below consists of a question and two statements numbered 1 & 2.
You have to decide whether the data provided in the statements are sufficient to answer the question.
Rahim is riding upstream on a boat, from point A to B, at a constant speed. The distance from A to B is 30 km. One minute after Rahim leaves from point A, a speedboat starts from point A to go to point B. It crosses Rahim’s boat after 4 minutes. If the speed of the speedboat is constant from A to B, what is Rahim’s speed in still water?
1. The speed of the speedboat in still water is 30 km/hour.
2. Rahim takes three hours to reach point B from point A.- Statement 1 alone is sufficient to answer the question, but statement 2 alone is not sufficient
- Statement 2 alone is sufficient to answer the question, but statement 1 alone is not sufficient
- Each statement alone is sufficient
- Both statements together are sufficient, but neither of them alone is sufficient
- Statements 1 & 2 together are not sufficient
-
XAT 2023 Question Paper QA DI
Rajnish bought an item at 25% discount on the printed price. He sold it at 10% discount on the printed price. What is his profit in percentage?
-
XAT 2023 Question Paper QA DI
The problem below consists of a question and two statements numbered 1 & 2.
You have to decide whether the data provided in the statements are sufficient to answer the question.
In a cricket match, three slip fielders are positioned on a straight line. The distance between 1st slip and 2nd slip is the same as the distance between 2nd slip and the 3rd slip. The player X, who is not on the same line of slip fielders, throws a ball to the 3rd slip and the ball takes 5 seconds to reach the player at the 3rd slip. If he had thrown the ball at the same speed to the 1st slip or to the 2nd slip, it would have taken 3 seconds or 4 seconds, respectively. What is the distance between the 2nd slip and the player X?
1. The ball travels at a speed of 3.6 km/hour.
2. The distance between the 1st slip and the 3rd slip is 2 meters.- Statement 1 alone is sufficient to answer the question, but statement 2 alone is not sufficient
- Statement 2 alone is sufficient to answer the question, but statement 1 alone is not sufficient
- Each statement alone is sufficient
- Both statements together are sufficient, but neither of them alone is sufficient
- Statements 1 & 2 together are not sufficient
-
XAT 2023 Question Paper QA DI
Given \(A=|x+3|+|x-2|-|2 x-8|\). The maximum value of \(|A|\) is:
-
XAT 2023 Question Paper QA DI
\(ABC\) is a triangle with \(BC =5 . D\) is the foot of the perpendicular from \(A\) on \(BC\). \(E\) is a point on \(CD\) such that \(BE =3\). The value of \(A B ^2- A E ^ { 2 } + 6 C D\) is:
-
XAT 2023 Question Paper QA DI
The addition of 7 distinct positive integers is 1740. What is the largest possible “greatest common divisor” of these 7 distinct positive integers?
-
XAT 2023 Question Paper QA DI
Jose borrowed some money from his friend at simple interest rate of 10% and invested the entire amount in stocks. At the end of the first year, he repaid 1/5th of the principal amount. At the end of the second year, he repaid half of the remaining principal amount. At the end of third year, he repaid the entire remaining principal amount. At the end of the fourth year, he paid the last three years’ interest amount. As there was no principal amount left, his friend did not charge any interest in the fourth year. At the end of fourth year, he sold out all his stocks. Later, he calculated that he gained Rs. 97500 after paying principal and interest amounts to his friend. If his invested amount in the stocks became double at the end of the fourth year, how much money did he borrow from his friend?
-
XAT 2023 Question Paper QA DI
The Guava club has won 40% of their football matches in the Apple Cup that they have played so far. If they play another n matches and win all of them, their winning percentage will improve to 50. Further, if they play 15 more matches and win all of them, their winning percentage will improve from 50 to 60. How many matches has the Guava club played in the Apple Cup so far? In the Apple Cup matches, there are only two possible outcomes, win or loss; draw is not possible.
-
XAT 2023 Question Paper QA DI
Find the value of: \( \frac{\sin ^6 15^0+\sin ^6 75^0+6 \sin ^2 15^0 \sin ^2 75^0}{\sin ^4 15^0+\sin ^4 75^0+5 \sin ^2 15^0 \sin ^2 75^0} \)
- \(\sin 15^{\circ}+\sin 75^{\circ}\)
- \(6 / 5\)
- 1
- \(\sin 15^{\circ} \cos 15^{\circ}\)
- None of the above
-
XAT 2023 Question Paper QA DI
ABC is a triangle and the coordinates of A, B and C are (a, b-2c), (a, b+4c) and (-2a,3c) respectively where a, b and c are positive numbers. The area of the triangle ABC is:
-
XAT 2023 Question Paper QA DI
Five students appeared for an examination. The average mark obtained by these five students is 40. The maximum mark of the examination is 100, and each of the five students scored more than 10 marks. However, none of them scored exactly 40 marks. Based on the information given, which of the following MUST BE true?
- At least, three of them scored a maximum of 40 marks
- At least, three of them scored more than 40 marks
- At least, one of them scored exactly 41 marks
- At most, two of them scored more than 40 marks
- At least, one of them scored less than 40 marks
-
XAT 2023 Question Paper QA DI
Raju and Sarita play a number game. First, each one of them chooses a positive integer independently. Separately, they both multiply their chosen integers by 2, and then subtract 20 from their resultant numbers. Now, each of them has a new number. Then, they divide their respective new numbers by 5. Finally, they added their results and found that the sum is 16. What can be the maximum possible difference between the positive integers chosen by Raju and Sarita?
-
XAT 2023 Question Paper QA DI
A painter draws 64 equal squares of 1 square inch on a square canvas measuring 64 square inches. She chooses two squares (1 square inch each) randomly and then paints them. What is the probability that two painted squares have a common side?
- \(\frac{112}{2016}\)
- \(\frac{1}{3}\)
- \(\frac{512}{100034}\)
- \(\frac{3}{97}\)
- \(\frac{7}{108}\)
-
XAT 2023 Question Paper QA DI
Consider \(a_{n+1}=\frac{1}{1+\frac{1}{a_n}}\) for \(n=1,2, \ldots, 2008,2009\) where \(a_1=1\). Find the value of \(a_1 a_2+a_2 a_3+a_3 a_4+\cdots+a_{2008} a_{2009}\)
- \(\frac{2009}{1000}\)
- \(\frac{2009}{2008}\)
- \(\frac{2008}{2009}\)
- \(\frac{6000}{2009}\)
- \(\frac{2008}{6000}\)
-
XAT 2023 Question Paper QA DI
A non-flying ant wants to travel from the bottom corner to the diagonally opposite top corner of a cubical room. The side of the room is 2 meters. What will be the minimum distance that the ant needs to travel?
- 6 meters
- \((2 \sqrt{2}+2)\) meters
- \(2 \sqrt{3}\) meters
- \(2 \sqrt{6}\) meters
- \(2 \sqrt{5}\) meters
-
XAT 2023 Question Paper QA DI
Suppose Haruka has a special key \(\Delta\) in her calculator called delta key:
Rule 1: If the display shows a one-digit number, pressing delta key \(\Delta\) replaces the displayed number with twice its value.
Rule 2: If the display shows a two-digit number, pressing delta key \(\Delta\) replaces the displayed number with the sum of the two digits.
Suppose Haruka enters the value 1 and then presses delta key \(\Delta\) repeatedly. After pressing the \(\Delta\) key for 68 times, what will be the displayed number?
-
XAT 2023 Question Paper QA DI
A small jar contained water, lime and sugar in the ratio of 90:7:3. A glass contained only water and sugar in it. Contents of both (small jar and glass) were mixed in a bigger jar and the ratio of contents in the bigger jar was 85:5:10 (water, lime and sugar respectively). Find the percentage of water in the bigger jar?
-
XAT 2023 Question Paper QA DI
There are three sections in a question paper and each section has 10 questions. First section only has multiple-choice questions, and 2 marks will be awarded for each correct answer. For each wrong answer, 0.5 marks will be deducted. Any un-attempted question in this section will be treated as a wrong answer. Each question in the second section carries 3 marks, whereas each question in the third section carries 5 marks. For any wrong answer or un-attempted question in the second and third sections, no marks will be deducted. A student’s score is the addition of marks obtained in all the three sections. What is the sixth highest possible score?
-
XAT 2023 Question Paper QA DI
\(A B C D\) is a trapezoid where \(B C\) is parallel to \(A D\) and perpendicular to \(A B\). Kindly note that \(B C \lt A D\). \(P\) is a point on \(A D\) such that \(C P D\) is an equilateral triangle. \(Q\) is a point on \(B C\) such that \(A Q\) is parallel to \(P C\). If the area of the triangle CPD is \(4 \sqrt{3}\), find the area of the triangle ABQ.
-
XAT 2023 Question Paper QA DI
Separately, Jack and Sristi invested the same amount of money in a stock market. Jack’s invested amount kept getting reduced by 50% every month. Sristi’s investment also reduced every month, but in an arithmetic progression with a common difference of Rs. 15000. They both withdrew their respective amounts at the end of the sixth month. They observed that if they had withdrawn their respective amounts at the end of the fourth month, the ratio of their amounts would have been the same as the ratio after the sixth month. What amount of money was invested by Jack in the stock market?
-
XAT 2023 Question Paper QA DI
Let x and y be two positive integers and p be a prime number. If x (x – p) – y (y + p) = 7p, what will be the minimum value of x – y?
-
XAT 2023 Question Paper QA DI
Which of the following will BEST capture the relationship between GDP (x-axis) and Life Satisfaction (y-axis) of countries?
- \(y=x\)
- \(y=x^2\)
- \(y=\log (x)\)
- \(y=\frac{1}{x^2}\)
- \(y=e^x\)
Choice C
\(y=\log (x)\)
-
XAT 2023 Question Paper QA DI
Which of the following, about the four islands, can be BEST inferred from the graphs?
- Whenever affect balance increases, satisfaction with life decreases
- Whenever Pleasant activities increase, satisfaction with life decreases
- Whenever Religion increases, satisfaction with life decreases
- Whenever satisfaction with life increases, family also increases
- Index of monetization varies maximum in Niijhum Dwip
Choice E
Index of monetization varies maximum in Niijhum Dwip
-
XAT 2023 Question Paper QA DI
Which of the following site has the highest fishing to economic ratio?
- Gizo
- Chittagong
- Roviana
- Niijhum Dwip
- All four islands have equal dependence
Choice C
Roviana
-
XAT 2023 Question Paper QA DI
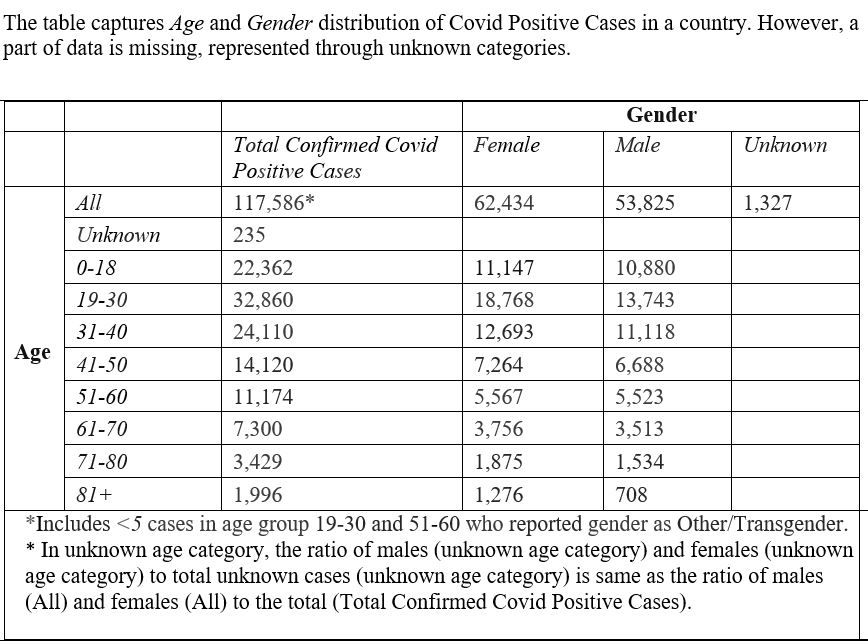
In unknown age category, the ratio of males (unknown age category) and females (unknown age category) to total unknown cases (unknown age category) is same as the ratio of males (All) and females (All) to the total (total confirmed covid positive cases). How many females were in the unknown age category (rounded to nearest integer)?
- 120
- 140
- 110
- 125
- 130
None
For this question, discrepancy was found in question/answer. Full Marks were awarded to all candidates.
-
XAT 2023 Question Paper QA DI
In which age category, the percentage of female covid patients is the HIGHEST?
- 61-70
- 31-40
- 41-50
- 51-60
- 81+
Choice E
81+
-
XAT 2023 Question Paper QA DI
Which of the following is true for “unknown gender Category”?
1. Unknown age group patients are less likely (percentage term) to provide information about gender than any other age category
2. Between 31 and 80, when age increases patients, in percentage terms, are less likely to provide information about gender
3. Elderly (81+) category patients are more likely to give information about gender than 0-18 age group- 3 only
- 2 only
- 1 and 2
- 1 and 3
- 2 and 3
None
For this question, discrepancy was found in question/answer. Full Marks were awarded to all candidates.
Go through the information given below, and answer the THREE questions that follow. islands, which have different levels monetization (Index). The Graph-3 captures levels of thirteen different socio-economic activities across four islands.
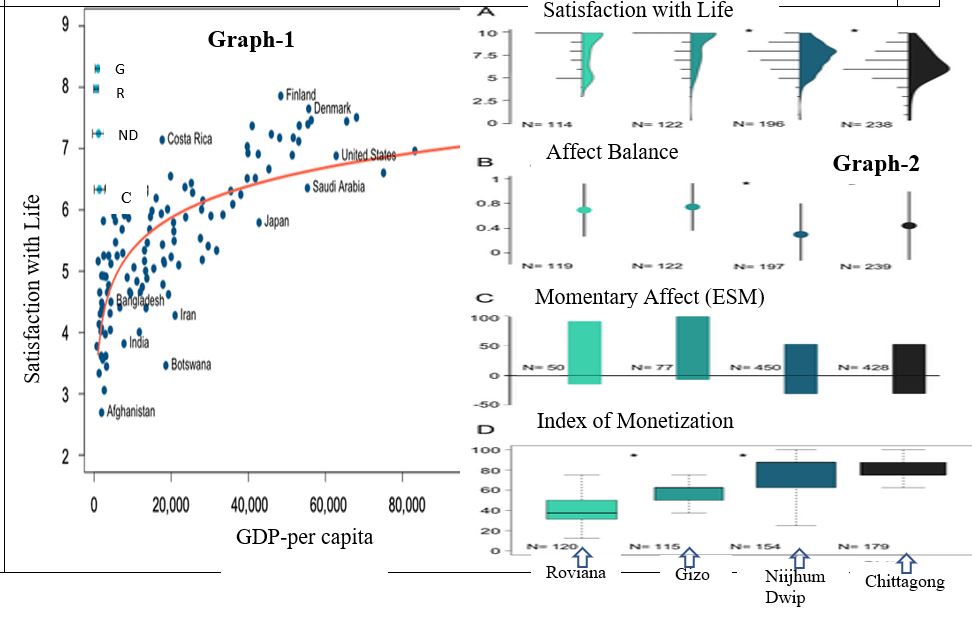
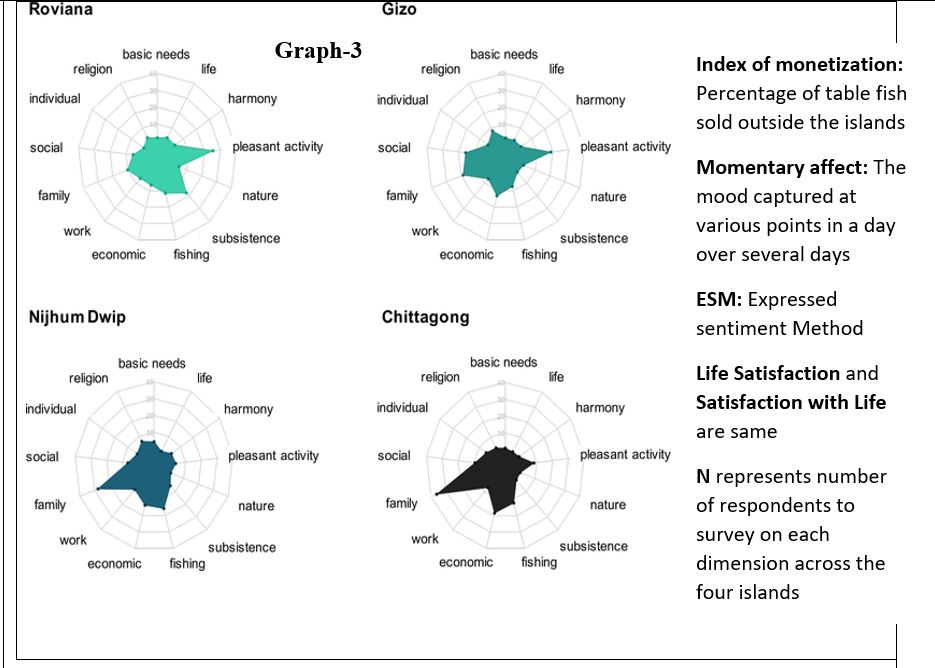
Go through the information given below, and answer the THREE questions that follow.