CAT 2022 Question Paper | Quant Slot 1

CAT Questions

CAT 2022 Quant was dominated by Arithmetic followed by Algebra. In Arithmetic, the questions were dominated by topics like Speed-time-distance, Mixture and Alligations. This year, there was a surprise. The questions from Geometry were relatively on the lower side as compared to the previous years. There were 8 TITA Qs this year. Overall this section was at a medium level of difficulty.

Question 22 : Let \(0 \leq a \leq x \leq 100\) and \(f(x)=|x-a|+|x-100|+|x-a-50|\). Then the maximum value of \(f(x)\) becomes 100 when \(a\) is equal to

---

---

Video Explanation

---

---

Explanatory Answer

f(x) = |x − a| + |x − 100| + |x − a − 50|
f(x) be re-written as |x − a| + |x − 100| + |x − (a+50)|
| x - a | signifies the distance between x and a.
| x - 100 | signifies the distance between x and 100.
| x - (a + 50) | signifies the distance between x and a + 50.
Since \( a \leq x \leq 100 \),
|x − a| + |x − 100| is just 100 - a and is independent of x

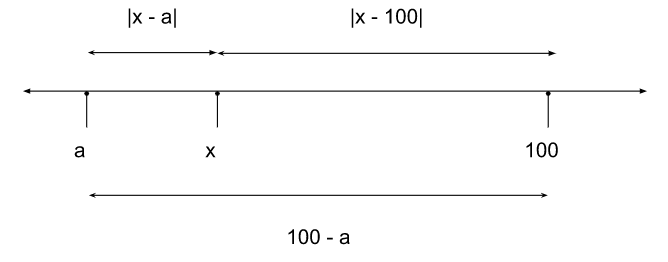
f(x) = |x − a| + |x − 100| + |x − (a+50)|
f(x) = (100 - a) + |x − (a+50)|
Now, let’s talk about |x − (a+50)|.
We know that \( x \geq a \), let us try to understand the maximum value that |x − (a+50)| can take.
x can be between a and (a + 50) or x can be to the right of (a + 50)
Case (i)
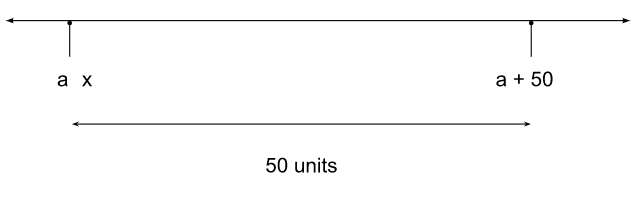
x is between a and (a + 50)
If this is the case, the maximum distance between a and (a+50) is just 50.
And this happens when x = a.
For any given value of ‘a’, We can just put ‘x’ at ‘a’ and make |x − (a+50)| equal to 50.

Case (ii)
x is to the right of (a + 50)
To find the maximum value that |x − (a+50)| can take, let us push x to the right most possible position and push (a + 50) to the left-most possible position.
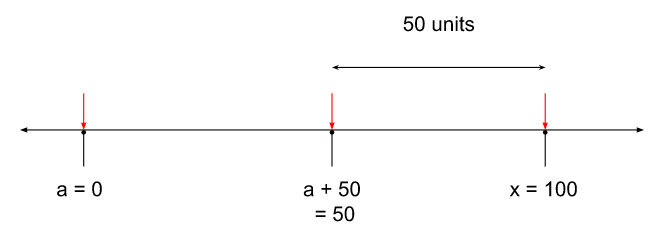
The right-most value that x can take is 100.
It looks like there is no hold on the left-most value that (a + 50) can take, but there is!
The left-most value that (a + 50) can take is dependent on the left-most value that ‘a’ can take. And the left-most value that ‘a’ can take is 0.
So in this extreme case of maximizing the distance between x and (a + 50),
a is at 0, (a+50) will be at 50, x is at 100
And the distance between x and (a + 50) is 50.

But why is understanding the maximum value that |x − (a+50)| can take important?
Once we establish the following two facts,
(i) |x − a| + |x − 100| is just 100 - a and is independent of x
(ii) For any given value of ‘a’, We can just put ‘x’ at ‘a’ and make |x − (a+50)| equal to 50.

For any given ‘a’, we can think of f(x) = |x − a| + |x − 100| + |x − (a+50)| as having a fixed part and a variable part.
Fixed part: |x − a| + |x − 100| = 100 - a
Whose value is fixed and does not change with the value of ‘x’

Variable part: |x − (a+50)|
Whose value can range from 0 to 50, based on the value of ‘x’

f(x) = (100 - a) + (something that reaches from 0 to 50)
If we need to fix the maximum value of f(x) at 100, we need to tackle the “worst-case scenario” that the ‘variable part’ can cause…
That is, we need to see f(x) = (100 - a) + (something that reaches from 0 to 50) as f(x) = (100 - a) + (something that is 50)
Now to cap f(x) at 100, (and also allow it take the value 100) we just need to set (100 - a) to 50, which happens when a = 50.
Therefore, a = 50.

---

The question is " Let \(0 \leq a \leq x \leq 100\) and \(f(x)=|x-a|+|x-100|+|x-a-50|\). Then the maximum value of \(f(x)\) becomes 100 when \(a\) is equal to "

Hence, the answer is '50'

Choice D is the correct answer.

Verbal Ability for CAT | CAT Reading Comprehension

Verbal Ability for CAT| CAT Para Jumble

Verbal Ability for CAT | CAT Sentence Elimination

Verbal Ability for CAT | CAT Paragraph Completion

Verbal Ability for CAT | CAT Critical Reasoning

Verbal Ability for CAT | CAT Word Usage

Verbal Ability for CAT| CAT Para Summary

Verbal Ability for CAT | CAT Text Completion

Verbal Ability for CAT | CAT Sentence Correction