XAT 2018 Question Paper | XAT QADI
XAT Quantitative Aptitude & Data Interpretation| XAT 2018 Question Paper
The best questions to practice for XAT Exam are the actual XAT Question Papers. 2IIM offers you exactly that, in a student friendly format to take value from this. If you would like to take the actual CAT papers inside a testing engine (for Free) head out here: CAT Official Question Mocks. In XAT 2018 we saw some beautiful questions that laid emphasis on Learning ideas from basics and being able to comprehend more than remembering gazillion formulae and shortcuts. Original XAT Question paper is the best place to start off your XAT prep practice. This page provides exactly that. To check out about 1000 CAT Level questions with detailed video solutions for free, go here: CAT Question Bank
-
XAT 2018 Question Paper - QADI
Find the value of the expression: 10 + 103 + 106 + 109
-
XAT 2018 Question Paper - QADI
Abdul, Bimal, Charlie and Dilbar can finish a task in 10, 12, 15 and 18 days respectively. They can either choose to work or remain absent on a particular day. If 50 percent of the total work gets completed after 3 days, then, which of the following options is possible?
- Each of them worked for exactly 2 days.
- Bimal and Dilbar worked for 1 day each, Charlie worked for 2 days and Abdul worked for all 3 days.
- Abdul and Charlie worked for 2 days each, Dilbar worked for 1 day and Bimal worked for all 3 days.
- Abdul and Dilbar worked for 2 days each, Charlie worked for 1 day and Bimal worked for all 3 days.
- Abdul and Charlie worked for 1 day each, Bimal worked for 2 days and Dilbar worked for all 3 days.
-
XAT 2018 Question Paper - QADI
If the diagonals of a rhombus of side 15 cm are in the ratio 3:4, find the area of the rhombus.
-
XAT 2018 Question Paper - QADI
The price of a product is P. A shopkeeper raises its price by X% and then offers a discount of Y% on the raised price. The discounted price again becomes P. If Y is the difference between X and Y, then find X.
-
XAT 2018 Question Paper - QADI
A mixture comprises water and liquids A and B. The volume of water is 1/3 of the total mixture and the volume of liquids A and B are in the ratio 5:3. To remove the water, the mixture is passed through a porous medium which completely absorbs the water and partially absorbs liquid A. Altogether this porous medium absorbs 200 ml of the initial mixture. If the ratio of volume of liquids A and B in the residual concentrated mixture becomes 7:9 then find the volume of water absorbed by the porous medium.
-
XAT 2018 Question Paper - QADI
A coin of radius 3 cm is randomly dropped on a square floor full of square shaped tiles of side 10 cm each. What is the probability that the coin will land completely within a tile? In other words, the coin should not cross the edge of any tile.
-
XAT 2018 Question Paper - QADI
It takes 2 liters to paint the surface of a solid sphere. If this solid sphere is sliced into 4 identical pieces, how many liters will be required to paint all the surfaces of these 4 pieces.
-
XAT 2018 Question Paper - QADI
Every day a person walks at a constant speed, V1 for 30 minutes. On a particular day, after walking for 10 minutes at V1 , he rested for 5 minutes. He finished the remaining distance of his regular walk at a constant speed, V2 , in another 30 minutes. On that day, find the ratio of V2 and his average speed
(i.e., total distance covered /total time taken including resting time).
-
XAT 2018 Question Paper - QADI
A boat, stationed at the North of a lighthouse, is making an angle of 30° with the top of the lighthouse. Simultaneously, another boat, stationed at the East of the same lighthouse, is making an angleof 45° with the top of the lighthouse. What will be the shortest distance between these two boats? The height of the lighthouse is 300 feet. Assume both the boats are of negligible dimensions.
-
XAT 2018 Question Paper - QADI
Two different quadratic equations have a common root. Let the three unique roots of the two equations be A, B and C - all of them are positive integers. If (A + B + C) = 41 and the product of the roots of one of the equations is 35, which of the following options is definitely correct?
- The common root is 29.
- The smallest among the roots is 1.
- One of the roots is 5.
- Product of the roots of the other equation is 5.
- All of the above are possible, but none are definitely correct.
-
XAT 2018 Question Paper - QADI
An antique store has a collection of eight clocks. At a particular moment, the displayed times on seven of the eight clocks were as follows: 1:55 pm, 2:03 pm, 2:11 pm, 2:24 pm, 2:45 pm, 3:19 pm and 4:14 pm. If the displayed times of all eight clocks form a mathematical series, then what was the displayed time on the remaining clock?
-
XAT 2018 Question Paper - QADI
The number of boys in a school was 30 more than the number of girls. Subsequently, a few more girls joined the same school. Consequently, the ratio of boys and girls became 3:5. Find the minimum number of girls, who joined subsequently.
-
XAT 2018 Question Paper - QADI
A girl travels along a straight line, from point A to B at a constant speed, V1 meters/sec for T seconds. Next, she travels from point B to C along a straight line, at a constant speed of V2 meters/sec for another T seconds. BC makes an angle 105° with AB. If CA makes an angle 30° with BC, how much time will she take to travel back from point C to A at a constant speed of V2 meters/sec, if she travels along a straight line from C to A?
-
XAT 2018 Question Paper - QADI
In the final semester, an engineering college offers three elective courses and one mandatory course. A student has to register for exactly three courses: two electives and the mandatory course. The registration in three of the four courses is: 45, 55 and 70. What will be the number of students in the elective with the lowest registration?
-
XAT 2018 Question Paper - QADI
X and Y are the digits at the unit's place of the numbers (408X) and (789Y) where X ≠ Y. However, the digits at the unit's place of the numbers (408X)63 and (789Y)85 are the same. What will be the possible value(s) of (X + Y)?
Example: If M = 3 then the digit at unit's place of the number (2M) is 3 (as the number is 23) and the digit at unit's place of the number (2M)2 is 9 (as 232 is 529).
-
XAT 2018 Question Paper - QADI
If 2 ≤ |x – 1|×|y + 3| ≤ 5 and both x and y are negative integers, find the number of possible combinations of x and y.
-
XAT 2018 Question Paper - QADI
David has an interesting habit of spending money. He spends exactly £X on the Xth day of a month. For example, he spends exactly £5 on the 5th of any month. On a few days in a year, David noticed that his cumulative spending during the last 'four consecutive days' can be expressed as 2N where N is a natural number. What can be the possible value(s) of N?
-
XAT 2018 Question Paper - QADI
A cone of radius 4 cm with a slant height of 12 cm was sliced horizontally, resulting into a smaller cone (upper portion) and a frustum (lower portion). If the ratio of the curved surface area of the upper smaller cone and the lower frustum is 1:2, what will be the slant height of the frustum?
-
XAT 2018 Question Paper - QADI
Two circles with radius 2R and √2R intersect each other at points A and B. The centers of both the circles are on the same side of AB. O is the center of the bigger circle and ∠AOB is 60°. Find the area of the common region between two circles.
- (√3 – π – 1)R2
- (√3 – π)R2
- (13π/6 + 1 - √3)R2
- (13π/6 + √3)R2
- None of the above
-
XAT 2018 Question Paper - QADI
Accordingly, choose the appropriate option given below the questions.
A group of six friends noticed that the sum of their ages is the square of a prime number. What is the average age of the group?
Statement I: All members are between 50 and 85 years of age.
Statement II: The standard deviation of their ages is 4.6.- Statement I alone is sufficient to answer.
- Statement II alone is sufficient to answer.
- Either of the statement is sufficient to answer.
- Both statements are required to answer.
- Additional information is required.
-
XAT 2018 Question Paper - QADI
Accordingly, choose the appropriate option given below the questions.
Harry and Sunny have randomly picked 5 cards each from a pack of 10 cards, numbered from 1 to 10. Who has randomly picked the card with number 2 written on it?
Statement I: Sum of the numbers on the cards picked by Harry is 5 more than that of Sunny.
Statement II: One has exactly four even numbered cards while the other has exactly four odd numbered cards.- Statement I alone is sufficient to answer.
- Statement II alone is sufficient to answer.
- Either of the statement is sufficient to answer.
- Both statements are required to answer.
- Additional information is required.
-
XAT 2018 Question Paper - QADI
Which of the following matches are yet to be played?
- Team A – Team B and Team C – Team D
- Team C – Team D and Team E – Team F
- Team E – Team F and Team B – Team D
- Team C – Team D and Team A – Team E
- Team A – Team B and Team E – Team F
Choice E
Team A – Team B and Team E – Team F
-
XAT 2018 Question Paper - QADI
How many students major in chemistry?
- Team A – Team D (1-0)
- Team A – Team E (2-1)
- Team B – Team D (1-0)
- Team C – Team F (2-0)
- None of the above
Choice B
Team A – Team E (2-1)
-
XAT 2018 Question Paper - QADI
Which of the following score line is not a possible outcome in the tournament?
- Team A – Team F (4-0)
- Team B – Team F (4-0)
- Team C – Team D (0-0)
- Team C – Team E (2-0)
- All of the above options are possible
Choice A
Team A – Team F (4-0)
-
XAT 2018 Question Paper - QADI
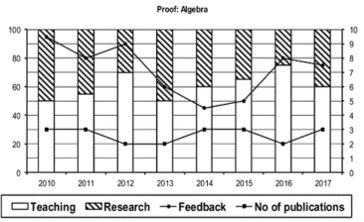
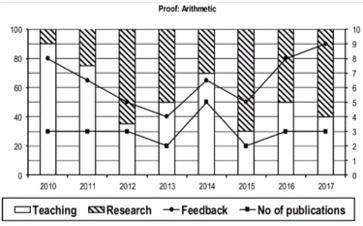
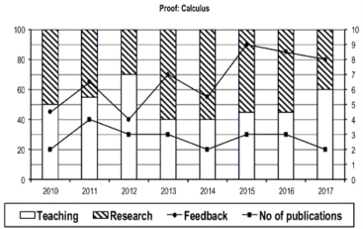
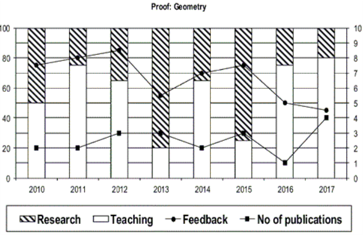
Which of the following, shows the maximum year to year percentage growth in feedback?
- Professor Arithmetic during 2013-2014
- Professor Algebra during 2015-2016
- Professor Calculus during 2012-2013
- Professor Calculus during 2014-2015
- None of the above
Choice C
Professor Calculus during 2012-2013
-
XAT 2018 Question Paper - QADI
Count the number of instances in which "annual decreasing efforts in research" is accompanied with "annual increase in feedback"?
- 5
- 7
- 9
- 11
- None of the above.
Choice C
9
-
XAT 2018 Question Paper - QADI
Research efficiency is the ratio of cumulative number of publication for a period of 3 years to the cumulative number of hours spent on research activity in those 3 years. Which of the following professors is the least efficient researcher for the period 2015 to 2017?
- Professor Arithmetic
- Professor Algebra
- Professor Geometry
- Professor Calculus
- Cannot be determined as research is expressed in percentage
Choice A
Professor Arithmetic
Questions 20 & 21 are followed by two statements each. These statements provide data that may help answer the respective questions. Read the questions and the statements and determine if the data provided by the statements is sufficient or insufficient, on their own or together, to answer the questions.
Six teams are playing in a hockey tournament where each team is playing against every other team exactly once. At an intermediate stage, the status is as follows:
| Teams | No. of matches played |
No. of matches won |
No. of matches lost |
No. of matches drawn |
Goals scored by the team |
Goals conceded by the team |
|---|---|---|---|---|---|---|
| Team A | 2 | 2 | 0 | 0 | 5 | 1 |
| Team B | 2 | 1 | 0 | 1 | 5 | 1 |
| Team C | 2 | 1 | 0 | 1 | 2 | 0 |
| Team D | 2 | 0 | 0 | 2 | 1 | 1 |
| Team E | 2 | 0 | 2 | 0 | 1 | 4 |
| Team F | 2 | 0 | 2 | 0 | 0 | 7 |
Notes:
1. The team that scores more goals than it concedes wins the match, while if both the teams score the same no. of goals, the match is declared drawn.
2. In a match played between Team X and Team Y , if team Xscores 1 and concedes none, then the score line would read: Team X-Team Y (1-0).
Which of the following score line is a possible outcome in the tournament?
The graphs below represent the performance of four professors, across years, measured on four variables: Percentage of time spent on teaching, percentage of time spent on research, feedback (on a scale of 10, right-hand side) and number of publications (right-hand side). Assume that the cumulative time spent per year on research and teaching activities are same for all four professors and each of them taught only one course of 90 classroom hours.