CAT 2021 Question Paper | Quant Slot 3

CAT 2021 Quant was dominated by Arithmetic followed by Algebra. In Arithmetic, the questions were dominated by topics like Speed-time-distance, Mixture and Alligations. This year, there was a surprise. The questions from Geometry were relatively on the lower side as compared to the previous years. There were 8 TITA Qs this year. Overall this section was at a medium level of difficulty.

Question 11 : Let ABCD be a parallelogram. The lengths of the side AD and the diagonal AC are 10 cm and 20 cm, respectively. If the angle ∠ADC is equal to 30° then the area of the parallelogram, in sq. cm, is

Video Explanation

Explanatory Answer

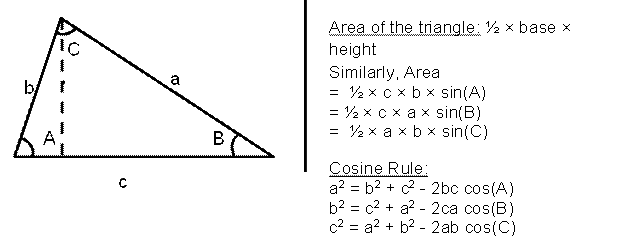
Revising the Cosine rule and the area of the triangle using the Sine rule…

We draw the described parallelogram ABCD.

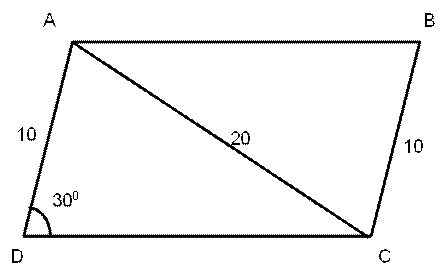
Applying the cosine rule in triangle ADC,
20² = 10² + DC² - 2(10)(DC) cos(30)
400 = 100 + DC² - 2(10)(DC)(\( \frac { \sqrt { 3 } } { 2 } \))
300 = DC² - (10)(DC)(\( \sqrt { 3 } \))
DC² - (10)(\( \sqrt { 3 } \))(DC) - 300 = 0
DC = \( \frac { ( \sqrt { 3 } ) ( 10 ) \pm \sqrt { ( \sqrt { 3 } 10 ) ^ { 2 } - 4 ( 1 ) ( - 300 ) } } { 2 } \)
DC is the length of one of the sides of the parallelogram, hence it can’t be negative.
DC = \( \frac { ( \sqrt { 3 } ) ( 10 ) + \sqrt { ( 300 ) 5 } } { 2 } \)
DC = \( \frac { \sqrt { ( 300 ) 5 } + ( \sqrt { 3 } ) ( 10 ) } { 2 } \)
DC = \( \frac { 10 \sqrt { 15 } + 10 \sqrt { 3 } } { 2 } \)
DC = 5(\( \sqrt { 15 } + \sqrt { 3 } \))
The are of the triangle ADC = ½ × DC × 10 × sin(30⁰) (Applying the sine rule)
Area(ADC) = ½ × DC × 10 × sin(30⁰)
Area(ADC) = \( \frac { 10 \mathrm { DC } } { 4 } \)= \( \frac { 5 D C } { 2 } \)
Area of the parallelogram ABCD = 2 × Area(ADC)
Area of the parallelogram ABCD = 2 × \( \frac { 5 D C } { 2 } \)
Area of the parallelogram ABCD = 5 (DC)
Area of the parallelogram ABCD = 5 ( 5(\( \sqrt { 15 } + \sqrt { 3 } \)))
Area of the parallelogram ABCD = 25(\( \sqrt { 15 } + \sqrt { 3 } \))

The answer is '\(25(\sqrt{3}+\sqrt{15})\)'

Choice D is the correct answer.