CAT 2022 Question Paper | Quant Slot 1

CAT Questions

CAT 2022 Quant was dominated by Arithmetic followed by Algebra. In Arithmetic, the questions were dominated by topics like Speed-time-distance, Mixture and Alligations. This year, there was a surprise. The questions from Geometry were relatively on the lower side as compared to the previous years. There were 8 TITA Qs this year. Overall this section was at a medium level of difficulty.

Question 10 : The largest real value of \(a\) for which the equation \(|x+a|+|x-1|=2\) has an infinite number of solutions for \(x\) is

---

---

Video Explanation

---

---

Explanatory Answer

We are given |x+a| + |x−1| = 2
|x - y| signifies the distance between the points x and y.
|x - (-a)| + |x−1| = 2
Is telling you that the sum of distances between the points x and (-a) and x and 1 is 2.
This implicitly means that the distance between (-a) and 1 can’t be more than 2 in the first place.
Imagine the distance between (-a) and 1 being more than 2.
For this explanation, let us assume that (-a) is to the left of 1.

In this case |x - (-a)| + |x−1| can never be equal to 2 and it will always be greater than 2.
So, the distance between (-a) and 1 can be exactly 2 units or less than 2 units.
Case i: distance between (-a) and 1 is less than 2 units.
Assume the distance between (-a) and 1 is less than 2 units and equal to some ‘x’ units
First of all x can’t be between (-a) and 1, because then |x - (-a)| + |x−1| will be lesser than 2.

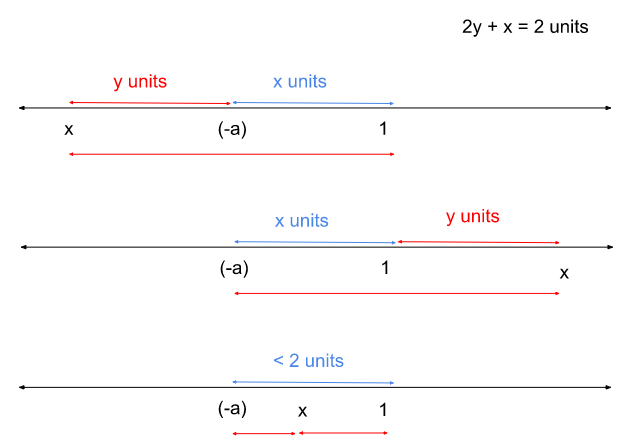
x can be y units to the left of (-a) or y units to the right of 1 such that 2y + x = 2 units. But there will just be 2 such solutions and not infinite solutions.
Case ii: distance between (-a) and 1 can be exactly 2 units.
x can only be between (-a) and 1 and can not be anywhere else.
Because if x is not between (-a) or 1, |x - (-a)| + |x−1| will be greater than 2.

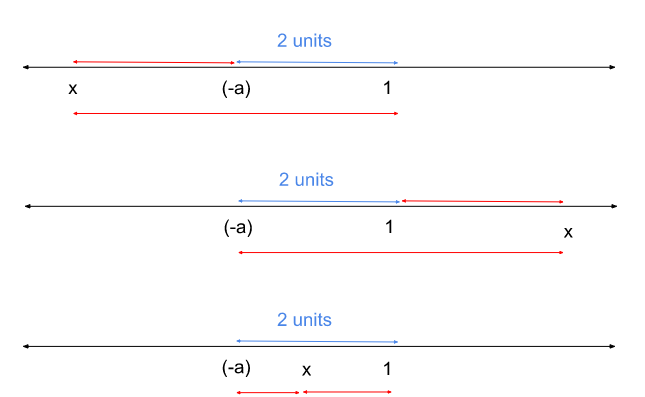
Since x can be anywhere between (-a) and 1, the value of |x - (-a)| + |x−1| will be exactly 2 units, this case satisfies the condition!
(-a) can be 2 units to the right of 1 or to the left of 1.
-a = -1
a = 1
(OR)
-a = 3
a = -3
The maximum value of a is 1.

---

The question is " The largest real value of \(a\) for which the equation \(|x+a|+|x-1|=2\) has an infinite number of solutions for \(x\) is "

Hence, the answer is '1'

Choice C is the correct answer.