CAT 2022 Question Paper | Quant Slot 2

CAT 2022 Quant was dominated by Arithmetic followed by Algebra. In Arithmetic, the questions were dominated by topics like Speed-time-distance, Mixture and Alligations. This year, there was a surprise. The questions from Geometry were relatively on the lower side as compared to the previous years. There were 8 TITA Qs this year. Overall this section was at a medium level of difficulty.

Question 1 : In triangle \(A B C\), altitudes \(A D\) and \(B E\) are drawn to the corresponding bases. If \(\angle B A C=45^{\circ}\) and \(\angle A B C=\theta\), then \(\frac{A D}{B E}\) equals

Video Explanation

Explanatory Answer

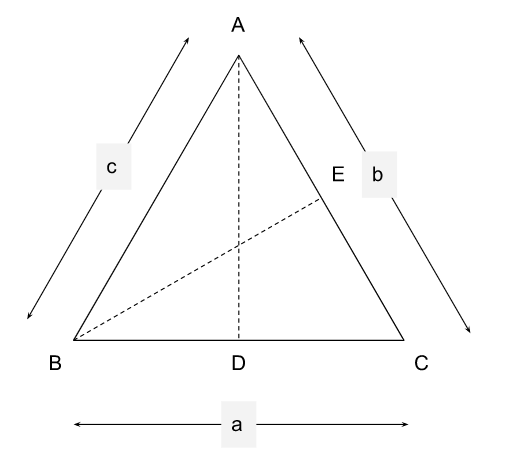
Let ‘a’, ‘b’ and ‘c’ be the length of the sides opposite to the vertices A, B and C respectively.
Let the area of the triangle be Δ.
By the sine rule,
Δ = \( \frac { 1 } { 2 } \times a \times c \times \sin ( B ) \)
Δ = \( \frac { 1 } { 2 } \times b \times c \times \sin ( A ) \)
This implies,
\( \frac { a } { b } = \frac { \sin ( B ) } { \sin ( A ) } = \frac { \sin ( \theta ) } { \sin ( 45 ) } = \sqrt { 2 } \sin ( \theta ) \)
Area of the triangle, Δ is also given by,
Δ = \( \frac { 1 } { 2 } \times a \times A D \)
Δ = \( \frac { 1 } { 2 } \times b \times B E \)
This implies,
\( \frac { a } { b } = \frac { A D } { B E } \)
\( \frac { a } { b } = \frac { A D } { B E } = \sqrt { 2 } \sin ( \theta ) \)
\( \frac { A D } { B E } = \sqrt { 2 } \sin ( \theta ) \)

The question is " In triangle \(A B C\), altitudes \(A D\) and \(B E\) are drawn to the corresponding bases. If \(\angle B A C=45^{\circ}\) and \(\angle A B C=\theta\), then \(\frac{A D}{B E}\) equals "

Hence, the answer is '\(\sqrt{2} \sin \theta\)'

Choice A is the correct answer.