CAT 2023 Question Paper | Quant Slot 2

CAT Questions

CAT 2023 Quant was dominated by Algebra followed by Arithmetic. In Arithmetic, the questions were dominated by topics like Speed-time-distance, Mixture and Alligations. This year, there was a surprise. The questions from Geometry were relatively on the lower side as compared to the previous years. There were 8 TITA Qs this year. Overall this section was at a medium level of difficulty.

Question 19 : The area of the quadrilateral bounded by the \(Y\)-axis, the line \(x=5\), and the lines \(|x-y|-|x-5|=2\), is

---

---

Video Explanation

---

---

Explanatory Answer

\( | x - y | - | x - 5 | = 2 \)
let \( | x - 5 | = \Delta \) (Observe that \( \Delta \) is a non-negative number.)
\( x = \Delta + 5 \) or \( x = 5 - \Delta \)
\( | x - y | - \Delta = 2 \)
\( | x - y | = \Delta + 2 \)
\( y = x + \Delta + 2 \) or \( y = x - \Delta - 2 \)
So, four pairs of points satisfy the condition \( | x - y | - | x - 5 | = 2 \)
Case I )
\( x = \Delta + 5 \) & \( y = x + \Delta + 2 \)
In this case, x is at least 5.
\( y = x + \Delta + 2 = x + \Delta + 2 + 3 - 3 = 2 x - 3 \)
So, every point on the line \( y = 2 x - 3 \) where \( x \geq 5 \) satisfies the given condition.
Case II )
\( x = \Delta + 5 \) & \( y = x - \Delta - 2 \)
In this case, x is at least 5.
\( y = x - \Delta - 2 = \Delta + 5 - \Delta - 2 = 3 \)
So, every point on of the form \( ( x , 3 ) \) where \( x \geq 5 \) satisfies the given condition.
Case III )
\( x = 5 - \Delta \) & \( y = x + \Delta + 2 \)
In this case, the highest value of x Is 5.
\( y = x + \Delta + 2 = 5 - \Delta + \Delta + 2 = 7 \)
So, every point on of the form \( ( x , 7 ) \) where \( x \leq 5 \) satisfies the given condition.
Case IV )
\( x = 5 - \Delta \) & \( y = x - \Delta - 2 \)
In this case, the highest value of x Is 5.
\( y = x - \Delta - 2 = x + x - 5 - 2 = 2 x - 7 \)
So, every point on the line \( y = 2 x - 7 \) where \( x \leq 5 \) satisfies the given condition.
We are to find the area enclosed by the y-axis, x = 5 and the lines of \( | x - y | - | x - 5 | = 2 \).
Because the area we are interested is bounded by x = 0 (y-axis) and x = 5, 0 ≤ x ≤ 5.
So, we’ll only be concerned about Case III and Case IV.
A rough sketch of the bounded region looks like…

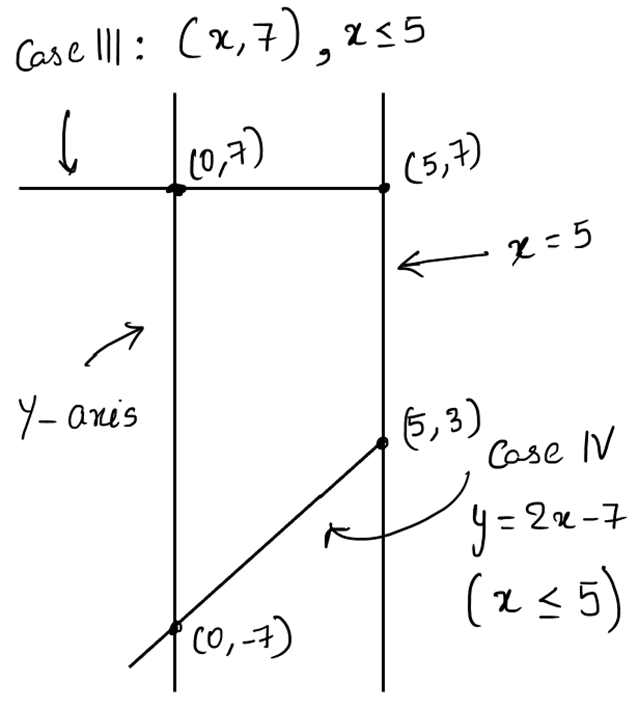
The line y = 2x – 7 touches x = 0 and x = 5 at (0, -7) and (5, 3) respectively.
So, the total area enclosed = \( 5 \times ( 7 + 7 ) - \frac { 1 } { 2 } \times 5 \times ( 3 + 7 ) = 45 \).
Some Suggestions:
● Notice that, since the area is bounded by x = 5, we know that x ≤ 5 and therefore the case where \( x = \Delta + 5 \) will never arise… which leaves us just with Case III and Case IV.
(We did Case I and Case II just for the solution to be thorough and complete.)
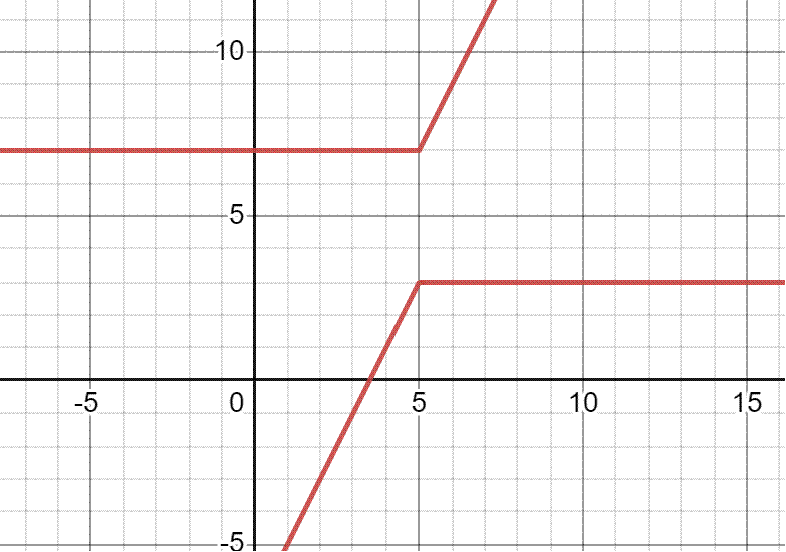
● Graphing the equations using graphing tools before visualizing is not advisable.
The graph of \( | x - y | - | x - 5 | = 2 \)looks like…

---

The question is " The area of the quadrilateral bounded by the \(Y\)-axis, the line \(x=5\), and the lines \(|x-y|-|x-5|=2\), is "

Hence, the answer is '45'