XAT 2021 Question Paper | XAT QADI
XAT Quantitative Aptitude & Data Interpretation| XAT 2021 Question Paper
The best questions to practice for XAT Exam are the actual XAT Question Papers. 2IIM offers you exactly that, in a student friendly format to take value from this. If you would like to take the actual CAT papers inside a testing engine (for Free) head out here: CAT Official Question Mocks. In XAT 2021 we saw some beautiful questions that laid emphasis on Learning ideas from basics and being able to comprehend more than remembering gazillion formulae and shortcuts. Original XAT Question paper is the best place to start off your XAT prep practice. This page provides exactly that. To check out about 1000 CAT Level questions with detailed video solutions for free, go here: CAT Question Bank
-
XAT 2021 Question Paper - QADI
Mohan has some money (₹M) that he divides in the ratio of 1:2. He then deposits the smaller amount in a savings scheme that offers a certain rate of interest, and the larger amount in another savings scheme that offers half of that rate of interest. Both interests compound yearly. At the end of two years, the total interest earned from the two savings schemes is ₹830. It is known that one of the interest rates is 10% and that Mohan deposited more than ₹1000 in each saving scheme at the start. What is the value of M?
-
XAT 2021 Question Paper - QADI
Mr. Jose buys some eggs. After bringing the eggs home, he finds two to be rotten and throws them away. Of the remaining eggs, he puts five-ninth in his fridge, and brings the rest to his mother’s house. She cooks two eggs and puts the rest in her fridge. If her fridge cannot hold more than five eggs, what is the maximum possible number of eggs bought by Mr. Jose?
-
XAT 2021 Question Paper - QADI
At any point of time, let x be the smaller of the two angles made by the hour hand with the minute hand on an analogue clock (in degrees). During the time interval from 2:30 p.m. to 3:00 p.m., what is the minimum possible value of x?
-
XAT 2021 Question Paper - QADI
One third of the buses from City A to City B stop at City C, while the rest go non-stop to City B. One third of the passengers, in the buses stopping at City C, continue to City B, while the rest alight at City C. All the buses have equal capacity and always start full from City A. What proportion of the passengers going to City B from City A travel by a bus stopping at City C?
-
XAT 2021 Question Paper - QADI
If log4m + log4n = log2(m + n), where m and n are positive real numbers, then which of the following must be true?
- No values of m and n can satisfy the five equation
- m = n
- \\frac{1}{m})+ \\frac{1}{n})= 2
- \\frac{1}{m})+ \\frac{1}{n})= 1
- \m^{2}+n^{2}=1)
-
XAT 2021 Question Paper - QADI
A small store has five units of a new phone model in stock: two white, two black, and one red. Three customers arrive at the shop to buy a unit each. Each one has a pre- determined choice of the colour and will not buy a unit of any other colour. All the three customers are equally likely to have chosen any of the three colours. What is the probability that the store will be able to satisfy all the three customers?
-
XAT 2021 Question Paper - QADI
Two circles P and Q, each of radius 2 cm, pass through each other’s centres. They intersect at points A and B. A circle R is drawn with diameter AB. What is the area of overlap (in square cm) between the circles R and P?
- 8π/ 3
- 17π/ 6 - \\sqrt{3})
- 8π/ 3 - \2 \sqrt{3})
- 17π/ 6 - \2 \sqrt{3})
- 13π/ 3 - \\sqrt{3})
-
XAT 2021 Question Paper - QADI
Swati can row a boat on still water at a speed of 5 km/hr. However, on a given river, it takes her 1 hour more to row the boat 12 km upstream than downstream. One day, Swati rows the boat on this river from X to Y, which is N km upstream from X. Then she rows back to X immediately. If she takes at least 2 hours to complete this round trip, what is the minimum possible value of N?
-
XAT 2021 Question Paper - QADI
The six faces of a wooden cube of side 6 cm are labelled A, B, C, D, E and F respectively. Three of these faces A, B, and C are each adjacent to the other two, and are painted red. The other three faces are not painted. Then, the wooden cube is neatly cut into 216 little cubes of equal size. How many of the little cubes have no sides painted?
-
XAT 2021 Question Paper - QADI
An encryption system operates as follows:
Step 1. Fix a number k (k≤26).
Step 2. For each word, swap the first k letters from the front with the last k letters from the end in reverse order. If a word contains less than 2k letters, write the entire word in reverse order.
Step 3. Replace each letter by a letter k spaces ahead in the alphabet. If you cross Z in the process to move k steps ahead, start again from A.
Example: k = 2: zebra --> arbez --> ctdgb.
If the word “flight” becomes “znmorl” after encryption, then the value of k:
-
XAT 2021 Question Paper - QADI
Let f(x) = \\frac{x^{2}+1}{x^{2}-1}) , if x ≠ 1, -1, and 1 if x = 1, -1. Let g(x) = \\frac{x+1}{x-1})if x ≠ 1 and 3 if x = 1.
What is the minimum possible value of \\frac{f(x)}{g(x)})?
-
XAT 2021 Question Paper - QADI
The average age of the female patients who weigh 50 kg or above is approximately
-
XAT 2021 Question Paper - QADI
The highest BMI among all patients is approximately
-
XAT 2021 Question Paper - QADI
The BMI of the oldest person considered as normal weight is approximately
-
XAT 2021 Question Paper - QADI
ABC is a triangle with integer-valued sides AB = 1, BC >1, and CA >1. If D is the mid- point of AB, then, which of the following options is the closest to the maximum possible value of the angle ACD (in degrees)?
-
XAT 2021 Question Paper - QADI
What BEST is known about the team compositions for the projects rated C?
- A two-member team
- A three-member team
- Either a three-member team or the six-member team
- Either a two-member team or a three-member team
- The six-member team
-
XAT 2021 Question Paper - QADI
What BEST is known about the team composition for the project rated A*?
- One is the six-member team, the rest are two-member teams.
- All are three-member teams.
- The three teams have two, three and six members respectively.
- All are two-member teams.
- All are either two-member or three-member teams.
-
XAT 2021 Question Paper - QADI
Total amount of money paid for projects rated A (in lakhs of Rupees) is:
-
XAT 2021 Question Paper - QADI
Rahul has just made a 3x3 magic square, in which the sum of the cells along any row, column or diagonal, is the same number N. The entries in the cells are given as expressions in x, y and z. Find N.
3x + 4y
2x
2x + y + z
\2 x^{2})
4y
\y^{2}) + z
y + z
3x + 2z
z - 1
-
XAT 2021 Question Paper - QADI
Rajesh, a courier delivery agent, starts at point A and makes a delivery each at points B, C and D, in that order. He travels in a straight line between any two consecutive points. The following are known: (i) AB and CD intersect at a right angle at E, and (ii) BC, CE and ED are respectively 1.3 km, 0.5 km and 2.5 km long. If AD is parallel to BC, then what is the total distance (in km) that Rajesh covers in travelling from A to D?
-
XAT 2021 Question Paper - QADI
Find z if it is knows that
a. -\y^{2}+x^{2})= 20
b. \y^{3}-2 x^{2}-4 z \geq-12)and
c. x, y and z are all positive integers
-
XAT 2021 Question Paper - QADI
The topmost point of a perfectly vertical pole is marked A. The pole stands on a flat ground at point D. The points B and C are somewhere between A and D on the pole. From a point E, located on the ground at a certain distance from D, the points A, B and C are at angles of 60, 45 and 30 degrees respectively. What is AB : BC : CD?
- (\3+\sqrt{3})) : (\1+\sqrt{3})) : 1
- (\\sqrt{3} - 1)) : 1 : (\3-\sqrt{3}))
- (\3-\sqrt{3})) : 1 : (\\sqrt{3} - 1))
- (\3-\sqrt{3})) : (\\sqrt{3} - 1)) : 1
- 1 : 1 : 1
-
XAT 2021 Question Paper - QADI
On the bank of the pristine Tunga river, a deer and a tiger are joyfully playing with each other. The deer notices that it is 40 steps away from the tiger and starts running towards it. At the same time, the tiger starts running away from the deer. Both run on the same straight line. For every five steps the deer takes, the tiger takes six. However, the deer takes only two steps to cover the distance that the tiger covers in three. In how many steps can the deer catch the tiger?
-
XAT 2021 Question Paper - QADI
Four friends, Ashish, Brian, Chaitra, and Dorothy, decide to jog for 30 minutes inside a stadium with a circular running track that is 200 metres long. The friends run at different speeds. Ashish completes a lap exactly every 60 seconds. Likewise, Brian, Chaitra and Dorothy complete a lap exactly every 1 minute 30 seconds, 40 seconds and 1 minute 20 seconds respectively. The friends begin together at the start line exactly at 4 p.m. What is the total of the numbers of laps the friends would have completed when they next cross the start line together?
-
XAT 2021 Question Paper - QADI
What is the number of happy male shoppers?
-
XAT 2021 Question Paper - QADI
Which among the following is the lowest?
- Number of unhappy first-time female shoppers
- Number of neutral first-time female shoppers
- Number of neutral first-time male shoppers
- Number of happy returning male shoppers
- Number of unhappy first-time male shoppers
-
XAT 2021 Question Paper - QADI
Which among the following cannot be determined uniquely?
- The number of first-time neutral male shoppers
- All the numbers can be determined uniquely
- The number of first-time happy male shoppers
- The number of returning male shoppers
- The number of returning unhappy female shoppers
-
XAT 2021 Question Paper - QADI
Zahir and Raman are at the entrance of a dark cave. To enter this cave, they need to open a number lock. Raman sees a note on a rock: “ ... chest of pure diamonds kept for the smart one ... number has six digits ... second last digit is 2, third last is 4 ... divisible by all prime numbers less than 15 ...”. Excited, Zahir and Raman seek your help: which of these can be the first digit of the six-digit number that will help them open the lock?
Read the following scenario and answer the three questions that follow.
The following plot describes the height (in cm), weight (in kg), age (in years) and gender (F for female, M for male) of 20 patients visiting a hospital.
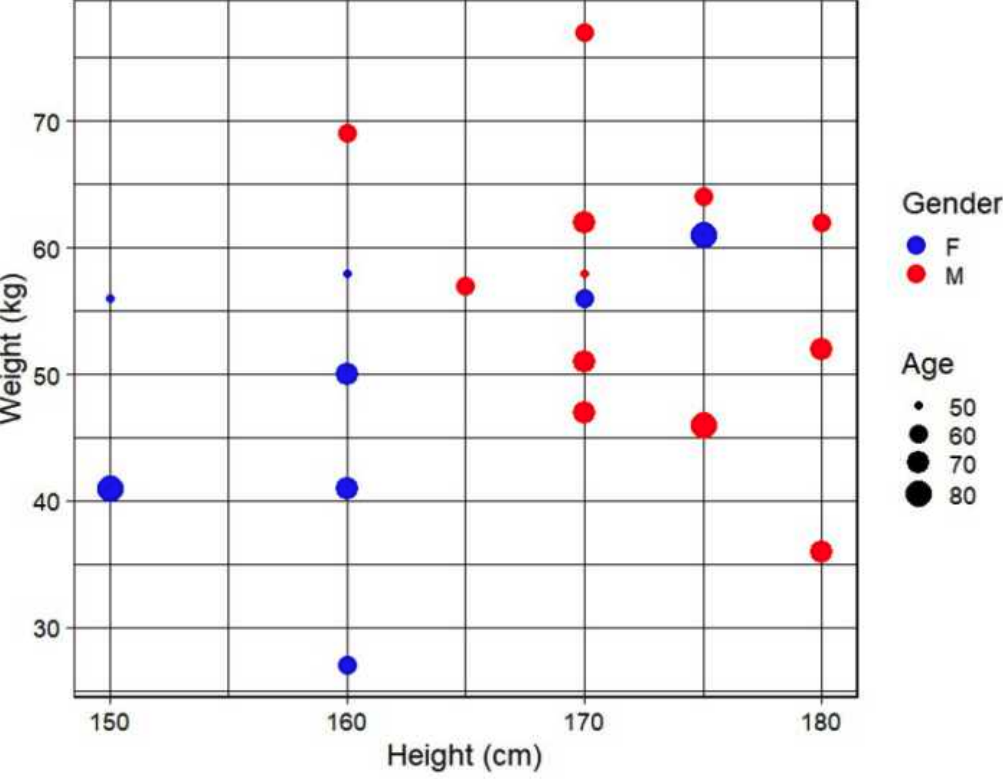
A person’s body mass index (BMI) is calculated as weight (in kg) divided by squared height (measured in square metres). For example, a person weighing 100 kg and of height 100 cm (1m) will have a BMI of 100. A person with BMI less than or equal to 18.5 is considered as underweight, above 18.5 but less than or equal to 25 as normal weight, above 25 but less than or equal to 30 as overweight, and above 30 as obese.
Read the following scenario and answer the three questions that follow.
A company awards incentives to its employees for successful project performances. It rates successful project performance in categories A*, A, B, and C. Employees, in solo projects rated A*, A, B, and C, are awarded incentives ₹6 lakh, ₹5 lakh, ₹3 lakh, and ₹1 lakh respectively. When a project has multiple team members, the following scheme is used to award the incentives:
| No. of team members |
Team lead gets |
Other members get |
| 1 |
100% |
|
| 2 |
90% |
70% |
| 3 |
80% |
50% each |
| 4 |
70% |
40% each |
| More than 4 |
Every member gets (200/n)% , where n = number of team members |
|
For example, for a project rated A, with three members, the team lead gets ₹4 lakh, and the other team members get ₹2.5 lakh each. A project always has a single team lead.
Six employees: Altaf, Bose, Chakrabarthi, Dipa, Ernie, and Fatima receive a total of ₹45 lakh in incentives by participating in a total of eight different projects that does not involve any other person. Not all six employees are involved in all eight projects.
The following are additionally known about these eight projects:
1. One project involves all six employees. Four projects involve three each, and the rest, two each.
2. Exactly three projects are rated C, for which a total of ₹4.8 lakh is paid.
3. Only one project is rated A*.
Read the following scenario and answer the three questions that follow.
A quick survey at the end of a purchase at buyagain.com asks the following three questions to each shopper:
1. Are you shopping at the website for the first time? (YES or NO) 2. Specify your gender: (MALE or FEMALE)
3. How satisfied are you? (HAPPY, NEUTRAL or UNHAPPY)
240 shoppers answer the survey, among whom 65 are first time shoppers. Furthermore:
i. The ratio of the numbers of male to female shoppers is 1 : 2 while the ratio of the numbers of unhappy, happy and neutral shoppers is 3 : 4 : 5
ii. The ratio of the numbers of happy first-time male shoppers, happy returning male shoppers, unhappy female shoppers, neutral male shoppers, neutral female shoppers and happy female shoppers is 1 : 1 : 4 : 4 : 6 : 6
iii. Among the first-time shoppers, the ratio of the numbers of happy male, neutral male, unhappy female and the remaining female shoppers is 1 : 1 : 1 : 2, while the number of happy first-time female shoppers is equal to the number of unhappy first-time male shoppe


