CAT 2024 Question Paper | Quant Slot 1

CAT Questions

CAT 2024 Quant was dominated by Algebra followed by Arithmetic. In Arithmetic, the questions were dominated by topics like Speed-time-distance, Mixture and Alligations. This year, there was a surprise. The questions from Geometry were relatively on the lower side as compared to the previous years. There were 8 TITA Qs this year. Overall this section was at a medium level of difficulty.

Question 4 :In the \(X Y\)-plane, the area, in sq. units, of the region defined by the inequalities \(y \geq x+4\) and \(-4 \leq x^2+y^2+4(x-y) \leq 0\) is

---

---

Video Explanation

---

---

Explanatory Answer

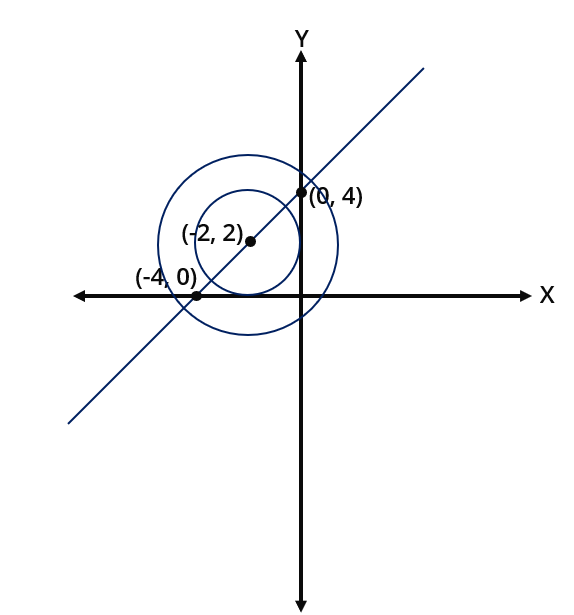
\(y \geq x+4\) represents the portion above the line \(y=x+4\) whose intercepts are \((-4,0)\) and \((0,4)\) \[ \begin{array}{c} -4 \leq x^2+y^2+4(x-y) \leq 0 \\ -4 \leq x^2+y^2+4 x-4 y \leq 0 \\ -4 \leq x^2+4 x+y^2-4 y \leq 0 \\ 4 \leq x^2+4 x+4+y^2-4 y+4 \leq 8 \\ 4 \leq(x+2)^2+(y-2)^2 \leq 8 \end{array} \] is the region between the two concentric circles with centre \((-2,2)\) and radii \(2 \sqrt{ } 2\) and 2

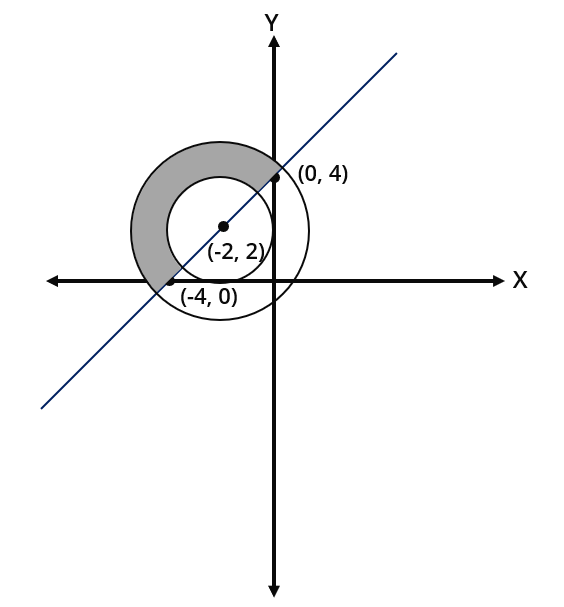
Thus, the common region is shaded in the diagram Hence, the area of the shaded region \[ \begin{array}{l} =\frac{1}{2}\left[\pi(2 \sqrt{2})^2-\pi(2)^2\right] \\ =\frac{1}{2}[8 \pi-4 \pi] \\ =\frac{1}{2}[4 \pi] \\ =2 \pi \end{array} \]

---

The question is "In the \(X Y\)-plane, the area, in sq. units, of the region defined by the inequalities \(y \geq x+4\) and \(-4 \leq x^2+y^2+4(x-y) \leq 0\) is"

Hence, the answer is '\(2 \pi\)'

Choice B is the correct answer.

Verbal Ability for CAT | CAT Reading Comprehension

Verbal Ability for CAT| CAT Para Jumble

Verbal Ability for CAT | CAT Sentence Elimination

Verbal Ability for CAT | CAT Paragraph Completion

Verbal Ability for CAT | CAT Critical Reasoning

Verbal Ability for CAT | CAT Word Usage

Verbal Ability for CAT| CAT Para Summary

Verbal Ability for CAT | CAT Text Completion

Verbal Ability for CAT | CAT Sentence Correction