IIFT 2018 Question Paper | IIFT Quants
IIFT Quantitative Aptitude | IIFT 2018 Question Paper
The best way to boost your IIFT prep is to practice the actual IIFT Question Papers. 2IIM offers you exactly that, in a student friendly format to take value from this. In the 2018 IIFT, quants were a mixed bag of questions of varying difficulty, with some routine questions and the others were very demanding. Some beautiful questions that laid emphasis on Learning ideas from basics and being able to comprehend more than remembering gazillion formulae and shortcuts.
-
IIFT 2018 Question Paper Quants
A Business Group has 3 Companies X, Y, Z and a Trust P which is engaged in charitable activities. Each group company has to donate 5% of its own funds to the Trust, excluding the loan which the company has taken from other companies of the group. X has given a loan to Y which is equivalent to 10% of the funds of Y. After receiving the loan, Y has funds which are 2 times the funds of Z. If Z gave Rs. 10,000 as donation to the Trust P, how much is the approximate contribution of 'Y' to the Trust P?
-
IIFT 2018 Question Paper Quants
A bucket contains 200cc of liquid. A solid ball is dropped in the bucket resulting in the rise of liquid level to 1.3 times of its original level. If the radius of the base of the bucket is 3 cm and the radius of the surface of the liquid level is 1 cm more than the radius of the base of the bucket before the ball is dropped. Find the volume of the solid metal ball.
-
IIFT 2018 Question Paper Quants
P...........Q
R...........S
T...........U
V..........W
Using 5 dots in each of the lines PQ, RS, TU, and VW as the vertices, how many triangles can be drawn such that the base is on any
one of the above lines?
-
IIFT 2018 Question Paper Quants
In the triangle PQR, S is the midpoint of QR. X is any point on PR. T is the point on QR such that PT || SX. If the area of triangle PQR is 5.8 sq. cm. then the area of triangle RTX is
-
IIFT 2018 Question Paper Quants
Given P(x,y) = x2 + xy +y2; Q(x,y) = x2 - xy +y2.
Then find the value of P(7, Q(9 , 4))
-
IIFT 2018 Question Paper Quants
In the given figure, PA = QB and PRQ is the arc of the circle, the centre of which is O such that angle POQ = 90°. If AB= \25 \sqrt{2}) cm and the perpendicular distance of AB from centre O is 30cm. Find the area of the shaded region?
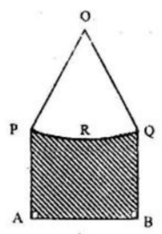
- 625\\sqrt{2})sq. cm
- 625 ( \\frac{1}{2}+\frac{\pi}{4}) )sq. cm
- 750\\sqrt{2}) - 625 (\\frac{1}{2}+\frac{\pi}{4}))sq. cm
- None
-
IIFT 2018 Question Paper Quants
The roots of quadratic equation y2-8y+14 = 0 are \\alpha) and\\beta). Find the value of (1 + \\alpha+\beta^{2})) ( 1 + \\beta+\alpha^{2}))
-
IIFT 2018 Question Paper Quants
\\frac{1}{\log _{x} y z+1}+\frac{1}{\log _{y} x z+1}+\frac{1}{\log _{x} x y+1}) = ?
-
IIFT 2018 Question Paper Quants
Ram, Ravi and Ratan can alone finish an assignment in 9 days, 12 days and 15 days respectively. They decide to complete a work by working in turns. Ram works alone on Monday, Ravi does the work alone on Tuesday, followed by Ratan working alone on Wednesday & so on. What proportion of the complete work is done by Ravi?
-
IIFT 2018 Question Paper Quants
Let \S_{1}) be a square of side 4 cm. Circle \C_{1}) circumscribes the square \S_{1}) such that all its corners are on \C_{1}). Another square \S_{2}) circumscribes the circle \C_{1}). Circle \C_{2}) circumscribes the square \S_{2}), and square \S_{3}) circumscribes circle \C_{2}), & so on. If \A_{N}) is the area between the square \S_{N}) and the circle \C_{N}), where N is the natural number. then the ratio of sum of all \A_{N}) to \A_{1}) is
-
IIFT 2018 Question Paper Quants
Joseph diametrically crosses a semi-circular playground and takes 48 seconds less than if he crosses the playground along the semi-circular path. If he walks 50 metres in one minute, the diameter of playground is
-
IIFT 2018 Question Paper Quants
Garima had only Rs. 200. Rs. 500 and Rs. 2000 notes in her wallet. She goes to Shoppers Stop. purchases some dresses and gives half of her Rs. 2000 notes & in turn receives the same number of Rs. 200 notes. She then goes to a restaurant and gives all her Rs. 500 notes and receives thirty Rs. 2000 notes, which increases the number of Rs. 2000 notes she had by 75%. Now if she has fifty Rs. 200 notes. What was the original number of Rs. 2000 and Rs. 200 notes she had at the start?
-
IIFT 2018 Question Paper Quants
A metallic solid is made up of a solid cylindrical base with a solid cone on its top. The radius of the base of the cone is 5 cm. and the ratio of the height of the cylinder and the cone is 3:2. A cylindrical hole is drilled through the solid with height equal to 2/3rd of the height of solid. What should be the radius (in cm) of the hole so that the volume of the hole is 1/3rd of the volume of the metallic solid after drilling?
- \\sqrt{\frac{45}{8}})
- \\sqrt{\frac{35}{8}})
- \\sqrt{\frac{65}{8}})
- \\sqrt{\frac{55}{8}})
-
IIFT 2018 Question Paper Quants
Nitin installed an overhead tank on the roof of his newly constructed house. Three taps are connected to the tank: 2 taps A and B to fill the tank and one tap C to empty it. Tap A alone can fill the tank in 12 hours, while tap B alone takes one and a half times more time than tap A to fill the tank completely. Tap C alone can empty a completely filled tank in 36 hours. Yesterday, to fill the tank, Nitin first opened tap A, and then after 2 hours opened tap B also. However after 6 hours he realised that tap C was open from the very beginning. He quickly closes tap C. What will be the total time required to fill the tank?
- 8 hours 48 minutes
- 8 hours 30 minutes
- 9 hours 12 minutes
- 9 hours 36 minutes
-
IIFT 2018 Question Paper Quants
At the foot of the mountain, the angle of elevation of the summit at the top of the mountain is 45°. After ascending 100 metres, at a slope of 30° up the mountain towards the summit. the angle of elevation of the summit is 60°. Find the height of the summit.
- 50 (\\sqrt{3}+1))metres
- 50 (\\sqrt{5}+1))metres
- 50 (\\sqrt{3}+2))metres
- 50 \\sqrt{3})metres
-
IIFT 2018 Question Paper Quants
Land Cruiser Prado, the latest SUV from Toyota Motors, consumes diesel at the rate of \\frac{1}{400}\left\{\frac{1000}{x}+x\right\}) litres per Km. when travelling at the speed of x km/hr. The diesel costs Rs. 65 per litre and the driver is paid Rs. 50 per hour. Find the steady speed that will minimize the total cost of a 1000 km trip?
-
IIFT 2018 Question Paper Quants
In a survey on the viewership of the TV channels, 73% of those surveyed viewed at least one of the three Channels: Star Plus, Sab TV, and Sony. 38% of those surveyed viewed Star Plus, 39% viewed Sony, and 23% viewed Sab TV. 11% of all those surveyed viewed all the three channels. What percentage of those surveyed, viewed more than one of the three TV channels?
-
IIFT 2018 Question Paper Quants
A physical therapist of the Russian football team knows that the team will play 40% of its matches on artificial turf this season. Because of his vast experience, he knows that a football player's chances of incurring a knee injury is 50% higher if he is playing on artificial turf instead of grass. If the player's chances of a knee injury on artificial turf is 0.42, what is the probability that a football player with knee injury, incurred the injury while playing on grass?
-
IIFT 2018 Question Paper Quants
The square root of \1+x^{2}+\sqrt{1+x^{2}+x^{4}}) is
- \\frac{1}{\sqrt{2}}\left[\sqrt{1+x+x^{2}}+\sqrt{1-x+x^{2}}\right])
- \\frac{1}{\sqrt{2}}\left[\sqrt{1+x+x^{2}}-\sqrt{1-x+x^{2}}\right])
- \\frac{1}{\sqrt{2}}\left[\sqrt{1+x^{2}+x^{4}+x^{8}}\right])
- None of the above
-
IIFT 2018 Question Paper Quants
\\log _{2} x \cdot \log _{\frac{x}{64}} 2=\log _{\frac{x}{16}} 2); then x= ?


