IIFT 2018 Question Paper | Quants

The best way to boost your IIFT prep is to practice the actual IIFT Question Papers. 2IIM offers you exactly that, in a student friendly format to take value from this. In the 2018 IIFT, Quants was a mixed bag of questions of varying difficulty, with some routine questions and the others were very demanding. Some beautiful questions that laid emphasis on Learning ideas from basics and being able to comprehend more than remembering gazillion formulae and shortcuts.

Question 10 : Let \S_{1}) be a square of side 4 cm. Circle \C_{1}) circumscribes the square \S_{1}) such that all its corners are on \C_{1}). Another square \S_{2}) circumscribes the circle \C_{1}). Circle \C_{2}) circumscribes the square \S_{2}), and square \S_{3}) circumscribes circle \C_{2}), & so on. If \A_{N}) is the area between the square \S_{N}) and the circle \C_{N}), where N is the natural number. then the ratio of sum of all \A_{N}) to \A_{1}) is

1. 1
2. \\frac{\pi}{2}) - 1
3. Can't be determined
4. None of the above

Explanatory Answer

The side of the square is 4 cm.
When a circle inscribes a square, the ratio of the radius of the circle and the side of the square is 1 : \\sqrt{2})
Therefore the radius of C1 = \\frac{4}{\sqrt{2}}) = \2 \sqrt{2})

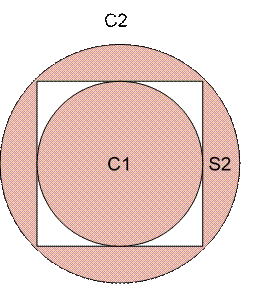
The ratio of the radius of the first circle C1 to second square is 1 : 2
The ratio of the side of the second square S2 to the radius of C2 is \\sqrt{2}: 1),
So, finally the ratio of radius of C1 to C2 will be 1 : \\sqrt{2})
Similarly the ratio of radii of C2 and C3 will also be 1 : \\sqrt{2})
So, the radii of the circles follows a geometric progression with common ratio \\sqrt{2})
Radius of C1 = \2 \sqrt{2})
Radius of C2 = 4
Radius of C3 = 4\\sqrt{2})
So radius of Cn = 2\\times \sqrt{2}^{n})

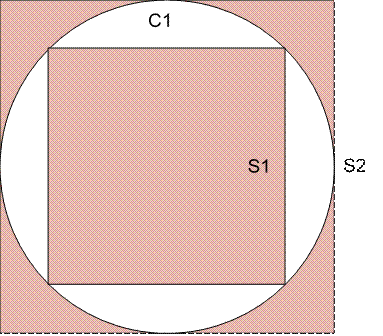
The ratio of the side of the Square S1 to the radius of the Circle C1 = \\sqrt{2}: 1)
The ratio of radius of the circle C1 to the side of the square S2 = 2 : 1.
So the ratio of the slides of S1 and S2 is 1 : \\sqrt{2})
Similarly the ratio of radii of S2 and S3 will also be 1 : \\sqrt{2})
So, the squares follow a geometric progression with common ratio \\sqrt{2})
Side of S1 = 4
Side of S2 = 4\\sqrt{2})
Side of S3 = 8
So Side of Sn = 4\\times \sqrt{2}^{n-1})
Now, the area between Cn and Sn = \A_{n})= (\\Pi \times r^{2})) - \a^{2})
= (\\Pi \times\left(2 \times \sqrt{2}^{n}\right)^{2})) - \\left(4 \times \sqrt{2}^{n-1}\right)^{2})
= \\left(\Pi \times 4 \times 2^{n}\right)-\left(16 \times 2^{n-1}\right))
= \\left(\Pi \times 4 \times 2^{n}\right)-\left(8 \times 2^{n}\right))
= \(\Pi-2)\left(4 \times 2^{n}\right))
\A_{n})= \(\Pi-2)\left(4 \times 2^{n}\right))
Area between S1 and C1 = \A_{1})= \(\Pi-2)\left(4 \times 2^{1}\right)) = \8(\Pi-2))
Sum of such n areas = \\sum 4(\Pi-2)\left(2^{n}\right)) = \4(\Pi-2) \times \Sigma\left(2^{n}\right)) = \8(\Pi-2)\left(2^{n}-1\right))
The question asks us the ratio between the Sum of all the intermediate areas to that of the a-rea between S1 and C1, which is
\\frac{8(\Pi-2)\left(2^{n}-1\right)}{8(\Pi-2)}) = \\left(2^{n}-1\right))

The answer is 'None of the above'

Choice D is the correct answer.

Verbal Ability for CAT | CAT Reading Comprehension

Verbal Ability for CAT| CAT Para Jumble

Verbal Ability for CAT | CAT Sentence Elimination

Verbal Ability for CAT | CAT Paragraph Completion

Verbal Ability for CAT | CAT Critical Reasoning

Verbal Ability for CAT | CAT Word Usage

Verbal Ability for CAT| CAT Para Summary

Verbal Ability for CAT | CAT Text Completion

Verbal Ability for CAT | CAT Sentence Correction