CAT 2020 Question Paper | DILR Slot 2

CAT Questions

The best questions to practice for CAT Exam are the actual CAT Question Papers. 2IIM offers you exactly that, in a student friendly format to take value from this. The questions in this Logical Reasoning set seen in CAT 2020 presents the idea of distributing beads in a grid, with a catch that the there is no one partiular arrangement. The idea of arrangements is taken one step further where we try to minimise the number of Blue beads in any arrangement, just like we maximised the Red beads in a question in this set. We take the given conditions in and generate a powerful idea on how we can set a grid which helps us in solving other questions in the set as well To check out about 1000 CAT Level questions with detailed video solutions for free, go here: CAT Question Bank

Twenty five coloured beads are to be arranged in a grid comprising of five rows and five columns. Each cell in the grid must contain exactly one bead. Each bead is coloured either Red, Blue or Green.

While arranging the beads along any of the five rows or along any of the five columns, the rules given below are to be followed:

1. Two adjacent beads along the same row or column are always of different colours.
2. There is at least one Green bead between any two Blue beads along the same row or column.
3. There is at least one Blue and at least one Green bead between any two Red beads along the same row or column.

Every unique, complete arrangement of twenty five beads is called a configuration.

Question 3 : What is the minimum number of Blue beads in any conguration?

---

---

Video Explanation

---

---

Explanatory Answer

The previous solution if done properly should have already answered this question. But if the previous one was not attempted then here is the way to solve this:
We need to include a minimum number of Bs in the grid, meaning, ideally we should include only 1 B per row. Let's attempt to do that.
Before we begin, what seems to be clear from the grid so far is that, if we are trying to maximize any colour, it is possible only if we move through the main diagonal. Clearly since that is not what we are trying to achieve for Bs, we should make sure that in the initial arrangement, B is not present in the middle cell / along the main diagonal
But while filling only 1 colour, we always move through the diagonal of the starting point. An initial arrangement might look like this:



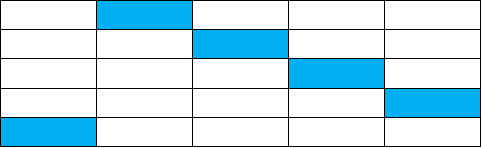
Now let's try to fill in colours and see what is feasible. While doing so, we need to keep in mind that since we are minimizing B, it automatically means we are trying to maximize R and . Which means that along the main diagonal should be beads with either R or G:



It might be tempting to stop here and answer 7. But we also need to try the other initial arrangement where we move B through the other remaining diagonal:



Let's try the same method of filling the main diagonal with either R or G. It is not feasible to use G in the main diagonal (can find out quickly by filling in the grid)
So the only feasible solution is:

---

The question is "What is the minimum number of Blue beads in any conguration?"

Hence, the answer is, " 6"