CAT 2020 Question Paper | Quants Slot 3

CAT Questions

This question is from Co-ordinate Geometry. Questions that appear in the CAT Exam from Co-ordinate Geometry tests an aspirant on the graphical representation Geometrical shapes, Distance between points, Section formula, Intercepts, Circles, and so on. In CAT Exam, one can generally expect to get approx. 1 question Coordinate Geometry. Make sure to a get good hold on this topic during your CAT Preparation. Practice CAT Question Paper from 2IIM CAT Question Bank and get a kick-ass CAT score.

Question 19 : The vertices of a triangle are (0,0), (4,0) and (3,9). The area of the circle passing through these three points is

---

---

Video Explanation

---

---

Explanatory Answer

A circle is circumscribed on the points (0,0) (4,0) and (3,9)
We are asked to find the area of this circle

We know that the area of a triangle with sides a, b and c, inscribed ina circle of radius R is given by
Area = \\frac{abc}{4R})

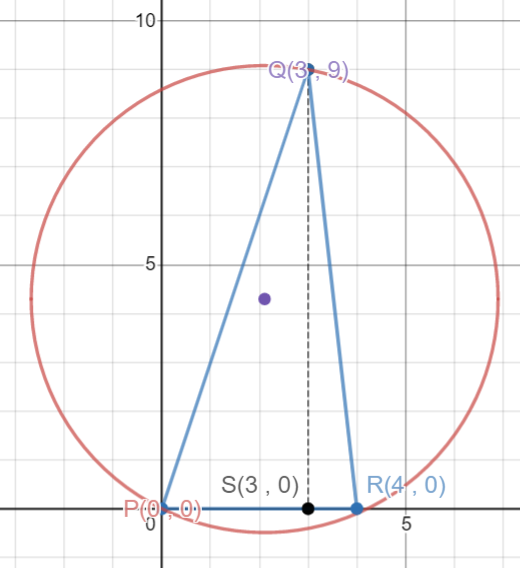
With the help of teh co-ordinates of the triangle it is easy to find the height of the triangle, which is QS = 9 units.
Hence the area of the triangle = A = \\frac{1}{2}) × base × height = \\frac{1}{2}) × PR × QS = \\frac{1}{2}) × 4 × 9 = 18 sq. units
a = PR = 4 units
b = QR = √(QS² + SR²) = √(9² + 1²) = √82
c = PQ = √(PS² + PQ²) = √(3² + 9²) = √90

W.K.T Area = \\frac{abc}{4R})
18 = \\frac{4 × √82 × √90}{4R})
R = \\frac{√205}{3})

Now that we know the radius of the circle the area of the circle = π × R² = π × \\frac{√205}{3}) × \\frac{√205}{3}) = π × \\frac{205}{9}) = \\frac{205π}{9})

---

The question is "The vertices of a triangle are (0,0), (4,0) and (3,9). The area of the circle passing through these three points is"

Hence, the answer is, "\\frac{205π}{9})"