CAT 2020 Question Paper | Quants Slot 1

CAT Questions

This question is from Geometry. It discusses about a circle that is inscribed in a rhombus. We need to find the ratio of the area of the circle to the area of the rhombus. Geometry is an important topic with lots of weightage in CAT exam. Make sure you master Geometry by practicing a lot of questions.

Question 18 : A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of the circle to the area of the rhombus is

---

---

Video Explanation

---

---

Explanatory Answer

Diagonals of a rhombus are perpendicular bisectors of each other
If diagonals are 12 and 16
Half of diagonals are 6 and 8 third side will become 10 = side of rhombus
Radius of the circle will be perpendicular to the side of the rhombus
Because side of the rhombus is tangent to the circle
The triangle is taken by half a diagonal (6) and (8) from the original figure


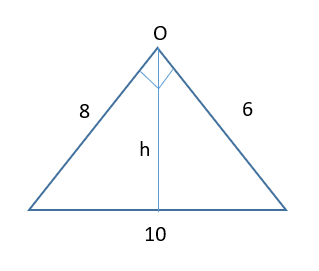
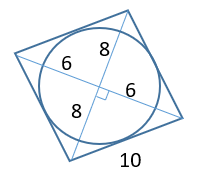
Just equating the areas
\\frac{1}{2}) × 8 × 6 = \\frac{1}{2}) × 10 × h
h = \\frac{24}{5}) = same as radius of the circle (r)
Now, area of circle : area of rhombus
π × \\frac{24}{5}) × \\frac{24}{5}) : \\frac{1}{2}) × 12 × 16
6π : 25

---

The question is "A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of the circle to the area of the rhombus is"

Hence, the answer is, "\\frac{6π}{25})"

Verbal Ability for CAT | CAT Reading Comprehension

Verbal Ability for CAT| CAT Para Jumble

Verbal Ability for CAT | CAT Sentence Elimination

Verbal Ability for CAT | CAT Paragraph Completion

Verbal Ability for CAT | CAT Critical Reasoning

Verbal Ability for CAT | CAT Word Usage

Verbal Ability for CAT| CAT Para Summary

Verbal Ability for CAT | CAT Text Completion

Verbal Ability for CAT | CAT Sentence Correction