CAT 2022 Question Paper | Quant Slot 3

CAT 2022 Quant was dominated by Arithmetic followed by Algebra. In Arithmetic, the questions were dominated by topics like Speed-time-distance, Mixture and Alligations. This year, there was a surprise. The questions from Geometry were relatively on the lower side as compared to the previous years. There were 8 TITA Qs this year. Overall this section was at a medium level of difficulty.

Question 18 : In a triangle \(\mathrm{ABC}, \mathrm{AB}=\mathrm{AC}=8 \mathrm{cm}\). A circle drawn with \(\mathrm{BC}\) as diameter passes through \(\mathrm{A}\). Another circle drawn with center at A passes through B and \(\mathrm{C}\). Then the area, in sq. \(\mathrm{cm}\), of the overlapping region between the two circles is

Video Explanation

Explanatory Answer

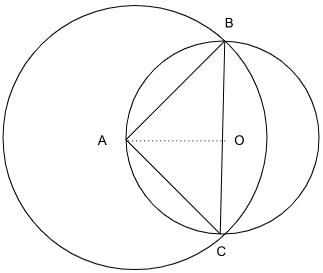
AB = AC = 8cm
Since BC is the diameter, angle A has to right-angled and angle B = angle C = 45 degrees.
Therefore, the radius of the circle centred at O is \( 4 \sqrt { 2 } \).
The radius of the circle centred at Aa is 8cm.
The common area between them = (half of the smaller circle) + (and the minor segment created by the chord BC in the bigger circle)
= \( \frac { 1 } { 2 } \pi ( 4 \sqrt { 2 } ) ^ { 2 } \) + (Ar(sector AOB) - Ar(AOB))
= \( 16 \pi \) + (Ar(sector AOB) - Ar(AOB))
= \( 16 \pi \) + (\( \frac { 1 } { 4 } \pi ( 8 ) ^ { 2 } \) - \( \frac { 1 } { 2 } * 8 * 8 \))
= \( 16 \pi + 16 \pi - 32 \)
= \( 32 \pi - 32 \)
= \( 32 ( \pi - 1 ) \)

The answer is '\(32(\pi-1)\)'

Choice B is the correct answer.