CAT 2017 Question Paper | Quants Slot 1

CAT Questions

This question is from CAT geometry. It discusses about a circular arc that has been drawn keeping a vertex of a triangle as a center. With the given data how can you find the area of the required region - Mr. Pythagoras might help you to start solving this problem! Give it a shot, and then watch the detailed video solution.

Question 17 : Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq. cm, of the region enclosed by BPC and BQC is :

1. 9π - 18
2. 18
3. 9π
4. 9

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Geometry

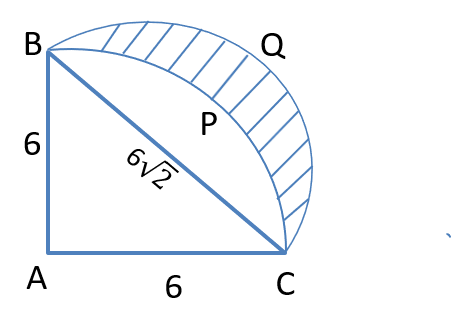
Given that ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC and let BPC be an arc of a circle centred at A and lying between BC and BQC.
If AB has length 6 cm then the area, in sq. cm, of the region enclosed by BPC and BQC has to be found.
i.e. the shaded region is,
Area of semicircle BQC = π (3√(2))²
= \\frac{18π}{2})
= 9π
Area of BPC = \\frac{π}{4}) × 6² - Area of triangle
= 9π - 9π - 18
= 18

The question is "Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq. cm, of the region enclosed by BPC and BQC is :"

Hence, the answer is 18

Choice B is the correct answer.