CAT 2017 Question Paper | Quants Slot 1

CAT Questions

Do you remember Pythagoras theorem? All of us have learned this concept well in our school days. And yeah, took the exams and passed. But when it comes to recalling the theorem after becoming adults, many of us fail (Ouch!). Here's a beautiful problem from CAT 2017 Question paper to commemorate the ground-breaking contribution by the cult of Euclidean geometry, Mr. Pythagoras. But wait this is not the end, this question also has a flavor of Speed, distance and time in it. Make sure you try this question before watching the video solution.

Question 20 :Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is: [TITA]

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Geometry

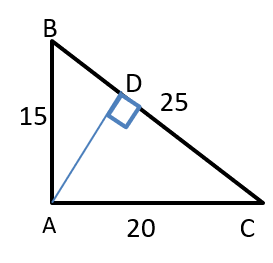
Given that ABC be a right-angled triangle with BC as the hypotenuse.
Lengths of AB and AC are 15 km and 20 km, respectively.
We have to find the minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour.
We should first find the minimum distance in order to find the minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour.
Therefore minimum distance AD has to be found and then it should be divided by the 30 km per hour.
Using the idea of similar triangles
Area of the triangle ABC
⟹ \\frac{1}{2}) × BA × AC = \\frac{1}{2}) × BC × AD
⟹ \\frac{1}{2}) × 15 × 20 = \\frac{1}{2}) × 25 × AD
⟹ AD = 12 units
Hence 12 kms is travelled at 30km per hour ⟹ \\frac{12}{30}) = \\frac{2}{5})
The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is \\frac{2}{5}) × 60 = 24 minutes
Key thing to be noted here is using Pythagoras theorem to find the altitude AD and then using Speed, Time and Distance formula to find the time.

The question is "Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is: [TITA]"

Hence, the answer is 24