CAT 2017 Question Paper | Quants Slot 1

CAT Questions

Permutation and Combination is a crucial topic in the CAT exam. This question talks about five diameters of a circle, but it has a flavor of permutation and combination hidden inside it. Will you be able to find that out? Give this question a shot and then watch how Rajesh has solved it.

Question 29 : Let AB, CD, EF, GH, and JK be five diameters of a circle with center at O. In how many ways can three points be chosen out of A, B, C, D, E, F, G, H, J, K, and O so as to form a triangle? [TITA]

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Permutation and Combination

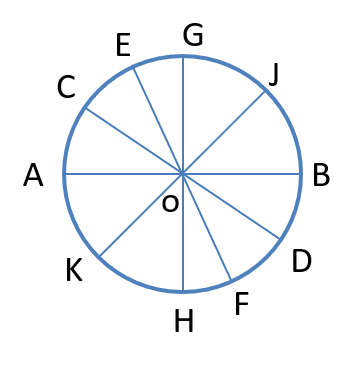
Given that AB , CD , EF , GH and JK be five diameters of a circle with center at O.
We have to find by how many ways three points can be chosen out of A , B , C , D , E , F , G , H , J , K and O so as to form a triangle.
We know that any three points lying on the circle are non collinear.
There are 11 points here we have to choose from any three points that are not collinear.
From these 10 points A, B, C, D, E, F, G, H, J, K we can select any three points on the circle such that they are non collinear. We can take O and then from remaining 10 we can take remaining two.
Since AOB , COD , GOH , EOF , JOK cannot form triangles, 5 can be subtracted.
¹⁰C₃ + ¹⁰C₂ - 5 = \\frac{10 × 9 × 8}{1 × 2 × 3}) + \\frac{10 × 9}{1 × 2}) - 5
⟹ 120 + 45 – 5 = 160 ways.

The question is "Let AB, CD, EF, GH, and JK be five diameters of a circle with center at O. In how many ways can three points be chosen out of A, B, C, D, E, F, G, H, J, K, and O so as to form a triangle? [TITA]"

Hence, the answer is 160