CAT 2018 Question Paper | Quants Slot 2
CAT Previous Year Paper | CAT Polynomials and Inequalities Questions | Question 14
CAT Questions This is a question from Polynomails that appeared in the CAT 2018 Question Paper. There are essentially two ways to solve the question. Try it yourself before looking at the video explanation where both the ways to solve this questionare explained.
To know about the exam's blueprint, visit 2IIM's CAT Blueprint.
Question 14 : The smallest integer n such that n3 - 11n2 + 32n - 28 ＞ 0 is [TITA]
🎉 Ace XAT 2025 with 2IIM's Crash Course - Enrol now
Best CAT Online Coaching
Try upto 40 hours for free
Learn from the
best!
2IIM : Best Online CAT Coaching.
Video Explanation
Best CAT Coaching in Chennai
CAT Coaching in Chennai - CAT 2022
Limited Seats Available - Register Now!
Explanatory Answer
Method of solving this CAT Question from Polynomials and Inequalities
We have to find the smallest integer n such that n3 - 11n2 + 32n - 28 > 0
For this we can assume some values for n, such that n = 10 , 9 , 8 ,.. so on and can find the smallest integer
n3 - 11n2 + 32n - 28 > 0
Let us now assume that n = 10
1000 – 1100 + 320 - 28 > 0
192 > 0 Hence this n = 10 works out
Similarly n = 9 , 8 also works so we can try out with n = 8 and if it works we can try for lower numbers otherwise we can try with 9
n3 - 11n2 + 32n - 28 > 0
512 – 704 + 256 – 28 > 0
36 > 0
Since n = 8 works lets check for n = 7
343 – 539 + 224 – 28 = 0
Hence the smallest integer was found to be 8
The other way of thinking about it can be by substituting it with smaller numbers and checking if something can factorize it
So \\frac{P(x)}{x-a}) where remainder = 0
Let's substitute n = 1 with n3 - 11n2 + 32n - 28
1 – 11 + 32 – 28 = -6 this doesn’t work and now we can substitute n = 2 and check it out
8 – 44 – 64 – 28 = 0
So this number n3 - 11n2 + 32n - 28 is a multiple of n-2
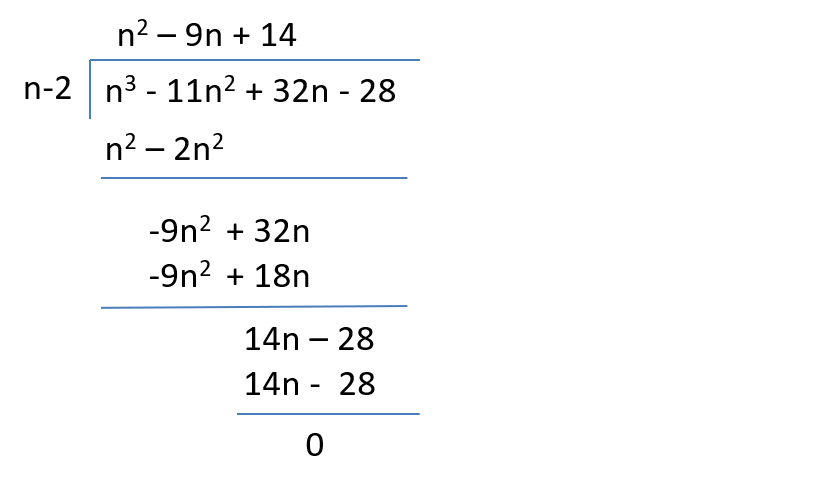
(n-2)(n2 – 9n + 14)
(n – 2)(n - 2)(n - 7) > 0
This will be greater than 0 when n = 7 and when n is between 2 and 7 it will be negative
When n = 1 ,
1 - 11 + 32 - 28 = -6 so this doesn’t work
Hence the smallest integer which will work is n = 8
The question is "The smallest integer n such that n3 - 11n2 + 32n - 28 ＞ 0 is [TITA]"
Hence, the answer is 8
