CAT 2018 Question Paper | Quants Slot 2

CAT Questions

It is almost a no-brainer that CAT Geometry must be mastered, and there's no escaping this topic in you online CAT Preparation. Over the years, the Geometry has been given huge emphasis, which makes it the second most important topic after Arithmetic. Visit 2IIM's CAT Blueprint to know more about what to expect in the upcoming CAT exam. Solve this question from CAT Previous Year Paper 2018 and ace your preparation.

Question 4 : On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is [TITA]

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Geometry

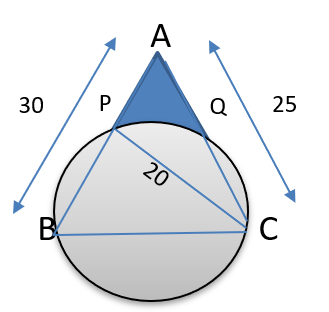
Let ABC be the triangle on which a circle of diameter BC is drawn, intersecting AB and AC at points P and Q respectively.The lengths of AB ,AC and CP are 30cm , 25cm and 20 cm respectively we have to find the length of BQ in cm.
Key thing here is ,this is semicircle so this angle P and Q should be 90° and now we are looking to do Pythagoras theorem



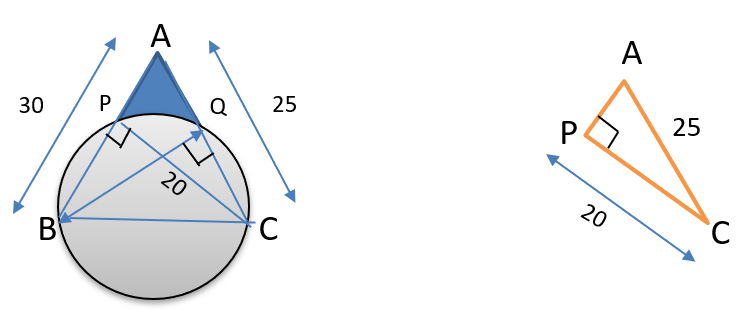
So think about triangle PAC, by Pythagoras theorem
AC² = AP² + PC² we can find that AP = 15



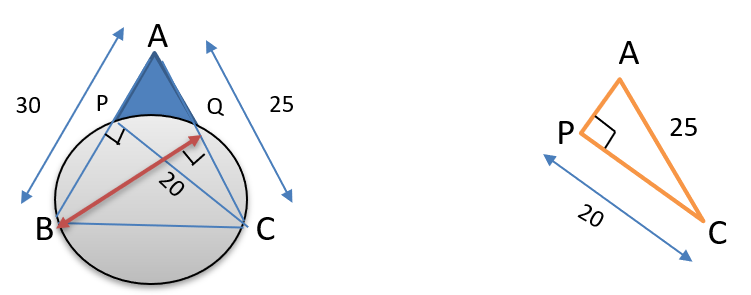
Since AP = 15 we can find BP by
AB = AP + PB
30 = 15 + PB
PB = 15
Now we can look at the triangle BPC, by Pythagoras theorem we can find that BC = 25



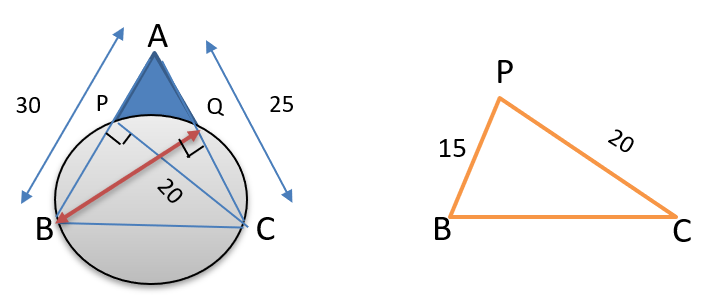
Now we have to find BQ .So we can take the area of the triangle formula which is equal to \\frac{1}{2}) × base × height
area of the triangle formula = \\frac{1}{2}) × base × height
\\frac{1}{2}) × AB × PC = \\frac{1}{2}) × AC × BQ
\\frac{1}{2}) × 30 × 20 = \\frac{1}{2}) × 25 × BQ
BQ = 24 cm

The question is "On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is [TITA] "

Hence, the answer is 24 cm