IIFT 2019 Question Paper | Quants

CAT Questions

The best way to boost your IIFT prep is to practice the actual IIFT Question Papers. 2IIM offers you exactly that, in a student friendly format to take value from this. In the 2019 IIFT, quants were a mixed bag of questions of varying difficulty, with some routine questions and the others were very demanding. Some beautiful questions that laid emphasis on Learning ideas from basics and being able to comprehend more than remembering gazillion formulae and shortcuts.

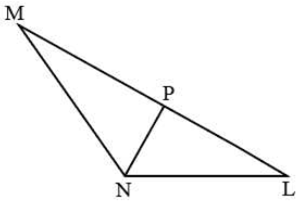
Question 15: In triangle MNL,line NP bisects the angle MNL. If NP : NL = 2 : 3 and angle MNL= 120 degrees . Then NP: NL: MN is:

---

---

Video Explanation

---

---

Explanatory Answer

We see that NP divides the angle MNL into two equal parts, so we use the angle bisector theorem.
So, $\frac{MP}{PL}$ = $\frac{MN}{NL}$

In triangle NPL, PN : NL :: 2x : 3x
So lets say PN : NL : LP :: 2x : 3x : kx

Using cosine rule we can say that,
cos 60 = $\frac{1}{2}$ = $\frac{2^2 + 3^2 - k^2}{2 ×2 ×3}$
5 = $\frac{1}{2}$ = $\frac{2^2 + 3^2 - k^2}{2 × 2 × 3}$
6 = 13 – k²


So, k = $\sqrt{7}$

Lets say the side MN is kx,
So, from angle bisector theorem:
$\frac{MP}{PL}$ = $\frac{MN}{NL}$
= $\frac{MP}{√7}$ = $\frac{kx}{3x}$
MP = $\frac{√7 × k}{3}$

Now in triangle MNP,
Using cosine rule:
Cos 60 = $\frac{1}{2}$ = $\frac{k^2 + 2^2 - (\sqrt{7}k /3)^2}{2 × 2 × k}$
We get
2 k = k² + 4 - $\frac{7}{9}$ k²
2 k = $\frac{2}{9}$ k² + 4
Solving this quadratic equation,
k²+ 18 = 9 k
(k-3)(k-6) = 0
So k could be 3 or 6
Since the triangle cannot be isosceles, k cannot be 3
So k = 6
This, PN : NL : LP :: 2x : 3x : 6x
Or PN : NL : LP :: 2 : 3 : 6

---

The question is "The ratio NP: NL: MN is:"

Hence, the answer is, "2:3:6"

Verbal Ability for CAT | CAT Reading Comprehension

Verbal Ability for CAT| CAT Para Jumble

Verbal Ability for CAT | CAT Sentence Elimination

Verbal Ability for CAT | CAT Paragraph Completion

Verbal Ability for CAT | CAT Critical Reasoning

Verbal Ability for CAT | CAT Word Usage

Verbal Ability for CAT| CAT Para Summary

Verbal Ability for CAT | CAT Text Completion

Verbal Ability for CAT | CAT Sentence Correction