IIFT 2019 Question Paper | Quants

CAT Questions

The best way to boost your IIFT prep is to practice the actual IIFT Question Papers. 2IIM offers you exactly that, in a student friendly format to take value from this. In the 2019 IIFT, quants were a mixed bag of questions of varying difficulty, with some routine questions and the others were very demanding. Some beautiful questions that laid emphasis on Learning ideas from basics and being able to comprehend more than remembering gazillion formulae and shortcuts.

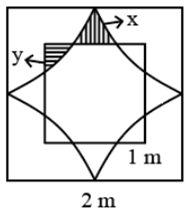
Question 19: A square of length 1 m is inside a square of length 2 m and four quarter circles are joined as shown in the figure. The value of (y-x) is given by

---

---

Video Explanation

---

---

Explanatory Answer

The area bounded between the Larger of the two squares and the four quarter circles will be
4 - 4 × \\frac{1}{4}) π r ²
and the radius of the circles will be 1, so the area becomes
4 - 4 × \\frac{1}{4}) π × 1 ²
4 - π
now if we subtract the area of the smaller of the two squares, the net area becomes
4 - π -1
= 3- π
which is the sum of 4 times of the difference between the shaded regions
4 × (x-y)
= 4 × (3 - π)
But, we need to find (y-x)
So, on dividing by 4 and taking the negative sign out we reach to (y-x)
= \\frac{π - 3}{4})

---

The question is "the value of (y-x) is:"

Hence, the answer is, "\\frac{(π - 3)}{4})"