CAT 2017 Question Paper | Quants Slot 2

CAT Questions

Functions form a part of Algebra in the Quantitative Aptitudeof the CAT Exam. Algebra forms around 12% of the total questions in this section and hence, you need practice for questions of these type. What better way than to go through the actual CAT Question Papers over the years and nail your online CAT preparation ? Start with this question now! Make sure you do not move onto the solution without solving the question yourself!
To know more about the pattern and type of questions asked in the CAT previous year paper, visit 2IIM's CAT Blueprint.

Question 32 : Let f(x) = 2x – 5 and g(x) = 7 – 2x. Then |f(x) + g(x)| = |f(x)| + |g(x)| if and only if

1. \\frac{5}{2}) < x < \\frac{7}{2})
2. x ≤ \\frac{5}{2}) or x ≥ \\frac{7}{2})
3. x < \\frac{5}{2}) or x ≥ \\frac{7}{2})
4. \\frac{5}{2}) ≤ x ≤ \\frac{7}{2})

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Functions

Given that f(x) = 2x – 5 and g (x) = 7 – 2x.
Consider the LHS,
|f(x) + g(x)| = |2x - 5 + 7 – 2x|
|2| = 2
So, RHS should also be 2.

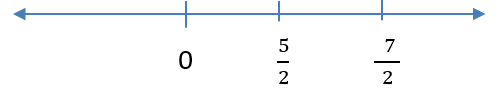
On considering the RHS, |f(x)| + |g(x)|, we get
\\frac{5}{2}) and \\frac{7}{2}) are the two pivotal points for which the values of f(x) and g(x) goes to zero.

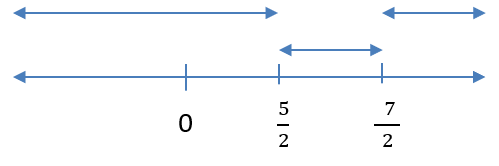
We have three ranges,
1) x < \\frac{5}{2}) or
2) \\frac{5}{2}) < x < \\frac{7}{2}) or
3) x > \\frac{7}{2}).
When x lies between 0 and \\frac{5}{2}),
|f(x)| + |g(x)| = 12 – 4x
When x lies between \\frac{5}{2}) < x < \\frac{7}{2}),
|f(x)| + |g(x)| = 2x – 5 + 7 – 2x = 2
When x is greater than \\frac{7}{2})
|f(x)| + |g(x)| = 2x – 5 + 2x – 7 = 4x – 12
Hence, out of these 3 possibilities, only \\frac{5}{2}) < x < \\frac{7}{2}) is equal to 2. So, this has to be our answer. But, is that so?
Let us consider when x = \\frac{5}{2}),
⟹ 12 – 4x = 12 – 4(\\frac{5}{2})) = 2
Similarly, when x = \\frac{7}{2}),
⟹ 4x – 12 = 4(\\frac{7}{2})) - 12 = 2
The value of |f(x)| + |g(x)| is equal to 2 even at x = \\frac{5}{2}) and x = \\frac{7}{2}).
Hence, the range is \\frac{5}{2}) ≤ x ≤ \\frac{7}{2})

The question is "Let f(x) = 2x – 5 and g(x) = 7 – 2x. Then |f(x) + g(x)| = |f(x)| + |g(x)| if and only if"

Hence, the answer is \\frac{5}{2}) ≤ x ≤ \\frac{7}{2})

Choice D is the correct answer