CAT 2018 Question Paper | Quants Slot 1

CAT Questions

One of the important aspects of CAT Online Preparation is solving CAT Previous year Paper . This question entails CAT Geometry concepts. Arcs, radii, triangles – what not? A typical CAT Geometry question from CAT Previous Year Paper, which would help you gain confidence after solving. Give it a try and watch the video solution.

Question 2 :In a circle with centre O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is

1. \\frac{π}{4})^{\\frac{1}{2})}
2. \\frac{π}{6})^{\\frac{1}{2})}
3. \\frac{π}{4√3})^{\\frac{1}{2})}
4. \\frac{π}{3√3})^{\\frac{1}{2})}

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Geometry

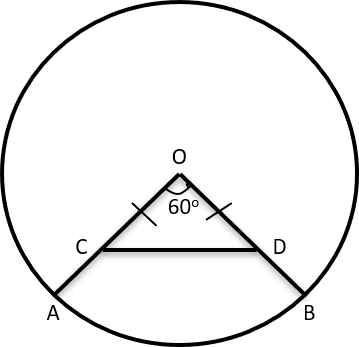
Given ∠AOB = 60°
Area of Sector AOB = \\frac{60}{360}) × π × 12 = \\frac{π}{6}) ---(1)
Given OC = OD => ∠OCD = ∠ODC = 60°
△OCD is an Equilateral Triangle with side = a
Area(△OCD) = \\frac{√3}{4}) × a × a ---(2)
Its given that Area(OCD) = \\frac{1}{2}) × Area(OAB)
a²\\frac{√3}{4}) = \\frac{π}{6×2})
a = (\\frac{π}{3√3}))^{\\frac{1}{2})}

The question is "In a circle with centre O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is"

Hence, the answer is \\frac{π}{3√3})^{\\frac{1}{2})} cm

Choice D is the correct answer.