CAT 2018 Question Paper | Quants Slot 1

CAT Questions

This is a fairly doable question from Functions. Though the question seems to be tricky, it is easy if one comprehends the basics of what is being asked. Solving these kinds of questions from the CAT Previous Year Paper gives you the essence of the difficulty tested in the CAT Exam.

Question 33 : Let f(x)=min{2x², 52 - 5x}, where x is any positive real number.Then the maximum possible value of f(x) is [TITA]

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Functions

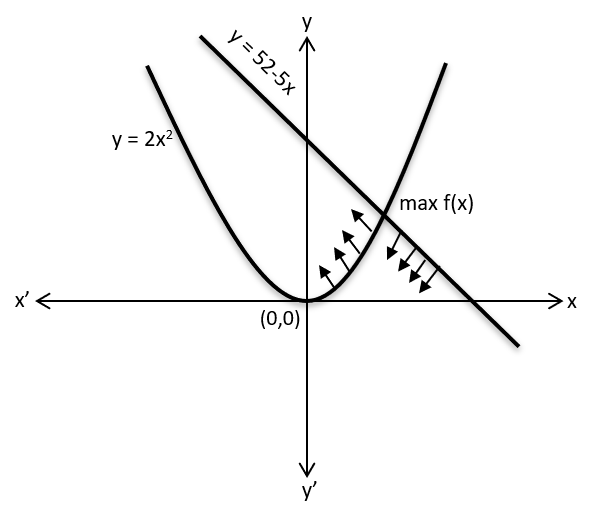
Given f(x) = min {2x², 52 − 5x}
From graph, we see that f(x) increases initially and then decreases after intersection
So, maximum value occurs when 2x² = 52 − 5x
2x² + 5x – 52 = 0
2x² - 8x + 13x - 52 = 0
2x(x-4) + 13(x-4) = 0
(2x+13) (x-4) = 0
Since x is a Positive real number, x = 4
min{2x²,52-5x} = min {32,32} = 32 = max f(x)

The question is " Let f(x)=min{2x², 52 - 5x}, where x is any positive real number.Then the maximum possible value of f(x) is [TITA]"

Hence, the answer is 32