CAT 2018 Question Paper | Quants Slot 1

CAT Questions

A classic square-in-square question from CAT 2018 Question paper that is slightly tricky, but gets simpler when you tackle it in the right way. Geometry is one of those topics that you cannot mess with and it requires intense practice. Solving CAT Previous Year Paper can be the way forward for you if you are stuggling with questions of his kind. Try your hand on this CAT Geometry question and assess yourself.

Question 24 :Points E, F, G, H lie on the sides AB, BC, CD, and DA, respectively, of a square ABCD. If EFGH is also a square whose area is 62.5% of that of ABCD and CG is longer than EB, then the ratio of length of EB to that of CG is:

1. 1 : 3
2. 4 : 9
3. 2 : 5
4. 3 : 8

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Geometry

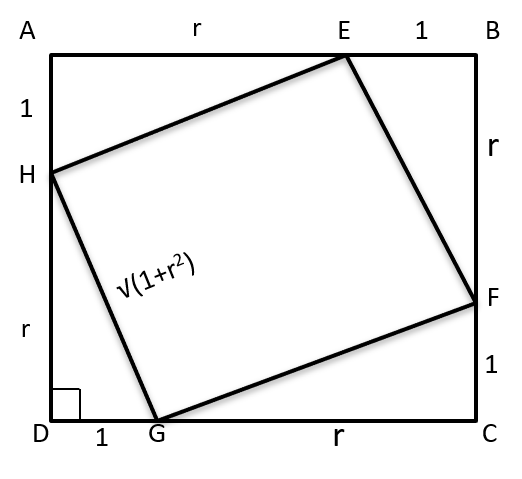
Given, Area(EFGH) = 62.5% Area(ABCD)
Area(EFGH) = \\frac{5}{8})Area(ABCD)
Let EB = 1 and CG = r
Similarly, the rest other dimensions are also of lengths 1 or r units
Applying pythagoras theorem on △DHG we get GH = √(1+r²)
Area(ABCD) = (1+r)² and Area(EFGH) = (√(1+r²))²
=> (1+r²) = \\frac{5}{8})(1+r)²

1 + r² = \\frac{5}{8})1+r²+2r)
8 + 8r² = 5 + 5r² + 10r
3r² – 10r + 3 = 0
(3r-1)×(r-3) = 0
r = \\frac{1}{3}) or r = 3
As CG > EB
r = 3 and ratio (EB : CG)= (1:r) = (1:3)

The question is "Points E, F, G, H lie on the sides AB, BC, CD, and DA, respectively, of a square ABCD. If EFGH is also a square whose area is 62.5% of that of ABCD and CG is longer than EB, then the ratio of length of EB to that of CG is:"

Hence, the answer is 1 : 3

Choice A is the correct answer.